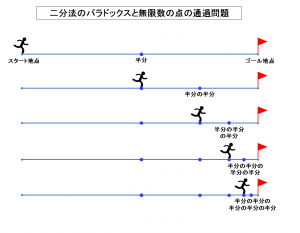
二分法のパラドックスとゴールに永久にたどり着けないランナーの話

以前に書いた、四回にわたる
ゼノンの存在の多数性論駁の議論では、

存在が多であると仮定すると矛盾が生じるので、
世界全体を包み込み、その基盤となっているような存在そのもの、
真に存在するものとしての存在は多ではなく一である

という背理法による
ゼノンの多数性論駁の議論を紹介しましたが、

エレアのゼノンの哲学的な業績としては、
この存在の多数性論駁の議論と並んで、

存在の運動性論駁の議論である

パラドックス（事実に反するはずの結論が、正しいように見える推論によって導かれてしまうことを示すことによって常識的な理解を覆す論法）

を用いた議論の方も有名で、

ゼノンが提示する一連の運動のパラドックスの議論は、
その全体をまとめて、

ゼノンのパラドックス（Zeno’s paradoxes）

とも呼ばれています。

そこで、今回から数回にわたって、
このゼノンのパラドックスにおける運動論駁の議論を
一つ一つ詳しく検討していきたいと思います。

まず、初回である今回紹介するのは、

競争路において走者が通過する
ゴールまでの目標地点の数をたとえに用いた

二分法（dichotomy、ディコトミー、二分割）

をテーマとした運動のパラドックスの議論です。

ゴールに永久にたどり着けないランナーの話

競争路における二分法のパラドックスについて、
自分が走路に立つランナーになった気持ちでイメージしてみると
それは、以下のような議論になります。

あなたは、競争路のスタート地点にランナーとして立っています。

ゴール地点までを見渡すとかなり距離があるので、

いきなりゴールまでは目指さずに、
まずは、スタートからゴールまでの距離を二分割した
ちょうど半分の地点を目指して走り出すことにします。

だいぶ走っていくと、
はじめの目標だったゴールまで半分の地点に到着します。

すると、ゴールまではまだ距離があるので、
今度も同じように、現在の地点からゴールまでの半分の地点を目標にして、
走っていくことにします。

現在いるのは、ゴールまであと半分の地点なので、新たに目指す地点は、
ゴールまで半分の地点のさらに半分の地点、
すなわち、ゴールまで半分の半分の地点ということになります。

そして、目標のゴールまで半分の半分の地点に到着したあなたは、
今度も同じように、現在の地点からゴールまでの半分の地点を目標にして、
さらに走り続けていくことになります。

現在いるのは、ゴールまで半分の半分の地点なので、
今度の目標は、ゴールまで半分の半分の半分の地点ということです。

こうして、ずっと走り続けているうちに、

あなたは、ふと、あることに気づきます。

常に、現在の地点からゴールまでの半分の地点を目標として走ることを
延々と繰り返していくと、

目標に到達するたびに、新たに到達すべき目標地点が現れるということが
際限なく続いていくことになり、

自分は、いつまでたってもゴールにたどり着けないことになりそうだが、
これはいったいどうしたことなのだろうか？

以上が、二分法のパラドックス（または競争路のパラドックス）における
ゼノンの運動論駁の議論の具体的内容となります。

無限数の点の通過問題と、運動の完遂の否定

少し議論を整理してまとめ直すと、
以下のようになります。

上図に示した通り、

スタート地点にいる走者がゴール地点に到達するためには、
その前に、今いるスタート地点とゴール地点の間を二つに等分した
半分の地点を通過しなければなりません。

そして、そのゴールまで半分の地点に到達したときには、
次は、そこからゴールまでの半分の地点である
ゴールまでの半分の半分の地点を通過しなければならない

というように、

ゴール地点へと到達するためには、

それ以前に、

ゴールまで半分の地点、
ゴールまで半分の半分の地点、
ゴールまで半分の半分の半分の地点…
を通過しなければならない

ということが無限に続いていくことになります。

新たな目標地点を通過するたびに、
走者は、どんどんゴールへと近づいていくことはできるのですが、

常に、目の前のゴールまであと半分の地点を考え続けることができる以上、

現在いる地点とゴール地点との半分の地点が
無限に生じていくことになり、

走者は、無限に生成し続ける
無限の数の点を通過しなければ、

ゴール地点へと到達することはできないことになりますが、
無限の数のものをすべて通過しきることは不可能なので、

走者は、競争路のゴール地点へと永久にたどり着くことができない
という結論になるのです。

つまり、

走者がゴール地点へと到達するためには、
それ以前に、ゴールまであと半分の目標地点として現れ続ける
無限の数の点を通過しなければなりませんが、

無限の数の点は、それが無限である以上、
有限の時間のなかでは、そのすべての点を通過し尽くすことは

論理的、原理的に不可能なので、

一度走りはじめた走者は
永遠にゴールへとたどり着くことができない

ということです。

そして、この議論に従えば、

あらゆる存在において、
ある地点から別の地点まで移動するという
運動の完遂自体があり得ないということになるので、

運動の完遂を否定することで、運動という概念自体を覆す
ゼノンの第一の運動のパラドックスの議論が完成することになるのです。

そして、

以上の二分法のパラドックスの議論の進化版が、
おそらくゼノンのパラドックスのなかでは最も有名な

「アキレスと亀のパラドックス」の議論ということになるのですが、

次回は、その「アキレスと亀のパラドックス」の議論
について考えていきたいと思います。

・・・

このシリーズの前回記事：
存在の多数性論駁④存在が無限大へと至る議論の問題点

このシリーズの次回記事：
アキレスと亀のパラドックス①無限数の点と無限回の試行回数

「エレアのゼノン」のカテゴリーへ