ローレンツ因子とは何か？ローレンツ因子γのピタゴラスの定理を用いた導出と宇宙船内で生じる時間の遅れの実際の計算
前回書いたように、特殊相対性理論に基づいて、光速に近い等速運動の状態にある宇宙船内において生じることになると考えられる時間の遅れは、
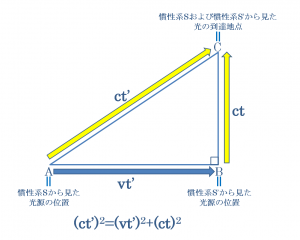
宇宙船内と地球上から見た光の進み方の違いを図示した直角三角形に対してピタゴラスの定理を用いることによって得られる関係式である(ct’)2=(vt’)2+(ct)2という数式を用いることによって具体的に計算することが可能であると考えられることになります。
そして、アインシュタインの特殊相対性理論においては、一般的に、基準となる慣性系Sに対して、慣性系Sとは異なる等速度運動の状態にある慣性系S’においては、
ローレンツ変換と呼ばれる不変的な時空座標の変換関係が成立すると考えられることになり、
相対性理論においては、こうしたローレンツ変換と呼ばれる座標の変換形式の内に現れるローレンツ因子γ
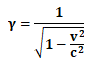
という係数に比例する形で慣性系S’の慣性系Sに対する時間の遅れや空間の収縮といった現象が生じると考えられることになるのですが、
こうした相対性理論における時空座標の変換形式の内で用いられるローレンツ因子と呼ばれる不変的な係数の値についても、
それは、前回取り上げたピタゴラスの定理を用いた関係式を利用する事によって直接的に導出することができる数値であると考えられることになります。
相対性理論におけるローレンツ因子のピタゴラスの定理を用いた導出
前回取り上げた光速に近い等速運動状態にある宇宙船の例においては、
宇宙船内と地球上から見た光の進み方の違いを図示した直角三角形に対してピタゴラスの定理を用いることによって得られる関係式から、
地球上の時間の進み方に対する宇宙船内の時間の進み方の遅れを導出することができることを示しましたが、それと同様に、
一般的に、
慣性系Sに対してx軸方向に速度vで移動している慣性系S’においては、それぞれの慣性系において観測される慣性系S’内の光の進み方の違いから、
慣性系Sにおける時間tと慣性系S’における時間t’の間には、下図のような直角三角形として示すことができる関係が成り立つと考えられることになります。
そして、詳しい説明は前回の記事で書いたものと全く同じになるので省きますが、
前回の場合と同様に、上記の直角三角形に対してピタゴラスの定理を用いることによって以下のような関係式を得ることができると考えられることになります。
すると、前回も取り上げた(ct’)2=(vt’)2+(ct)2という上記の関係式をそのままt’について展開していくことによって、
特殊相対性理論において慣性系Sに対して生じる慣性系S’における時間の遅れや空間の収縮のことを表す比例係数として用いられているローレンツ因子の値を導出することができると考えられることになるのです。
まず、
(ct’)2=(vt’)2+(ct)2
という上記の関係式をt’2についてまとめていくと、以下のように変形できます。
(ct’)2‐(vt’)2=(ct)2
c2t’2‐v2t’2=c2t2
t’2(c2‐v2)=c2t2
ここで、式を整理するために両辺をc2で割ると、
となり、さらにこの式をt’2について展開していくと、
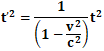という式が得られることになります。
そして、ここで、上記の式の両辺を平方根に開くと、
より、
最終的に、慣性系Sにおける時間tと慣性系S’における時間t’の間には、
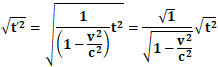すなわち、
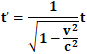
という関係が成り立つことが明らかとなります。
つまり、
相対性理論においては、上記の
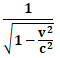
という係数に比例する形で、
慣性系Sに対してx軸方向に速度vで移動している慣性系S‘における時間の遅れが生じていくことになると考えられるということです。
そして、ピタゴラスの定理を用いた上記の数式によって導出されるこうした係数の値こそが、
一般的に、相対性理論における時空座標の変換形式として用いられるローレンツ変換において現れるローレンツ因子γ
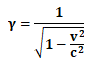
の正体であると考えられることになるのです。
ローレンツ因子を用いて算出する宇宙船内で生じる時間の遅れの実際の計算
ちなみに、
前回例として挙げた光速の60パーセントの速度である秒速約18万キロメートルで航行する宇宙船内において生じる地球上の時間に対する宇宙船内の時間の遅れについて、
それを今回導出したローレンツ因子の値を用いた数式によって改めて計算し直すと、以下のようになると考えられることになります。
条件より、
上記のローレンツ因子を用いた計算式
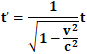
に対して、
光の速さc＝300000、宇宙船の速度v=180000を代入すると、
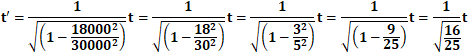となります。
ここで、
なので、
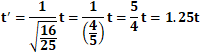となり、
地球から見た場合、光速の60パーセントの速度である秒速約18万キロメートルで航行する宇宙船内においては地球上よりも1.25倍時間が遅く進むと計算されることなり、
これは当然ながら、ピタゴラスの定理を用いた関係式から直接得られた前回の計算結果とぴったりと一致することになるのです。
・・・
次回記事：相対性理論ではどのような原理によって物体の長さが縮むのか？①光速に近い速度で飛ぶ宇宙船内の二つのライトの点灯の観測
前回記事：特殊相対性理論における時間の遅れのピタゴラスの定理を用いた計算方法
関連記事：ローレンツ変換とは何か？特殊相対性理論の相対性原理の方程式に基づくローレンツ変換の導出とローレンツ因子の意味
「物理学」のカテゴリーへ
「数学」のカテゴリーへ