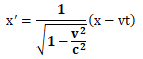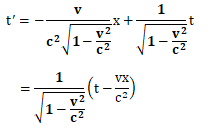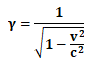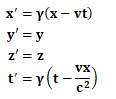ローレンツ変換とは何か？特殊相対性理論の相対性原理の方程式に基づくローレンツ変換の導出とローレンツ因子の意味

前回書いたように、特殊相対性理論の根本原理となる光速度不変の原理に基づく相対性原理は、

物理学的には、光速度不変の原理に基づいてすべての慣性系において光の運動を含むあらゆる物理法則が同等に成立することを意味することになりますが、

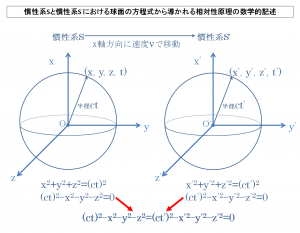
それは数学的には、慣性系Sの時空座標 (x, y, z, t)と慣性系S’の時空座標 (x’, y’, z’, t’)との間に不変的な座標の変換関係が成立しているということを意味することになります。

そして、こうした特殊相対性理論における相対性原理は、数学的な記述としては、

(ct)²-x²-y²-z²=(ct’)²-x’²-y’²-z’²=0

という式によって記述することができると考えられることになり、

上記の式を満たす普遍的な変換法則こそがローレンツ変換と呼ばれる座標の変換形式ということになるのですが、

こうしたローレンツ変換と呼ばれる時空座標の変換形式は、上記の相対性原理を表す方程式から具体的にどのような形で導出されることになると考えられることになるのでしょうか？

特殊相対性理論の相対性原理の方程式に基づくローレンツ変換の導出

まず、慣性系Sと慣性系S’の間で不変的な座標の変換関係が成立するというのは具体的にはどのようなことを意味するのか？ということについてですが、

それは、一言でいうと、

慣性系S’の時空座標(x’, y’, z’, t’)のそれぞれの値が、

慣性系Sの時空座標を表す(x, y, z, t)と、慣性系S’の慣性系Sに対する相対速度v、そして、相対性理論において不変数とされる光の速さcという

x, y, z, t, v, cという全部で6つの要素のみを文字として用いた不変的な一つの形式によってで記述することができるということを意味することになります。

つまり、

x’ =k₁x+k₂y+k₃z+k₄t
y’ =l₁x+l₂y+l₃z+l₄t
z’ =m₁x+m₂y+m₃z+m₄t
t’ =n_nx+n₂y+n₃z+n₄t

といった形式を満たす係数k₁～n₄を

上記の相対性原理を表す方程式

(ct)²-x²-y²-z²=(ct’)²-x’²-y’²-z’²=0

から導出することができればいいと考えられるということです。

しかし、

こうした連立方程式を解くための厳密な数学的解法は、基本的には高校数学の範囲を超えてしまうことになり、そのために必要な数学的処理もかなり複雑なものになってしまうので、ここでは省略して、

代わりに、上記の方程式を解く考え方の一つの指針や解法の大まかな流れのようなものを簡単に記述しておくことにします。

すると、冒頭の図でも示しているように、上記の方程式の前提において、

慣性系Sに対する慣性系S’の移動のあり方は、慣性系S’はx軸方向にのみ移動しているとされていて、y軸とz軸方向については変化していないということと、

慣性系Sからx軸方向に速度vで移動している慣性系S’において、慣性系S’の原点O’は慣性系Sの原点Oから見てx=vtの地点に位置しているということから、

慣性系S’の時空座標 (x’, y’, z’, t’)のそれぞれの値は、

x’=d(x−vt)
y’=y
z’=z
t’=ex+ft

といった形で表せると考えられることになり、

あとは、上記の形式を満たすような係数d,e,fを上記の方程式から求めればいいと考えられることになります。

ローレンツ変換を表す数式と相対性理論におけるローレンツ因子の意味

そして、以上のような指針に従って上記の方程式を順々に解いていくと、

結果として、慣性系Sの時空座標 (x, y, z, t)と慣性系S’の時空座標 (x’, y’, z’, t’)との間には、以下のような不変的な対応関係があることが示されることになります。

y’=y

z’=z

そして、上記の座標(x, y, z, t)から座標 (x’, y’, z’, t’)への不変的な変換関係においては、座標x’とt’に共通する係数が現れることになりますが、

この係数はローレンツ因子γと呼ばれていて、

としたうえで、上記の座標変換の形式を改めて書き直すと、それは以下のような形にまとめて記述することができます。

そして、上記の慣性系Sの時空座標 (x, y, z, t)から慣性系S’の時空座標 (x’, y’, z’, t’)への不変的な座標の変換形式のあり方こそが、ローレンツ変換と呼ばれる座標の変換形式であるということになるのです。

・・・

以上のように、

ローレンツ変換と呼ばれる座標の変換形式は、特殊相対性理論においては、上記のような過程を経ることによって、相対性理論を表す方程式から直接的に導き出すことができると考えられることになります。

そして、こうしたローレンツ変換と呼ばれる変換形式の特殊相対性理論における物理学的な意味は、一言でいうと、

上記のローレンツ因子と呼ばれる係数の値に比例する形で、空間や時間が伸び縮みしていくことにあると考えられることになるのです。

また、こうしたローレンツ因子の存在自体は、ピタゴラスの定理を用いることなどによって比較的簡単な数学的処理によって導出することができ、

それによって、特殊相対性理論の相対性原理に基づいて生じる空間や時間の伸び縮みの具体的なあり方も示すことができると考えられることになるのですが、

こうしたローレンツ因子についてのより具体的な数学的考察に入っていく前に、まず次回の記事では、上記の数式において示されているローレンツ変換やローレンツ因子といった相対性理論において必須となっている概念が、

なぜ相対性理論の提唱者であるアインシュタインの名ではなく、オランダの物理学者ローレンツの名が冠されることになっているのか？というローレンツ変換と相対性理論をめぐる物理学史的な経緯について改めて考えておきたいと思います。

・・・

次回記事：光の波動説におけるエーテル理論の隆盛とマクスウェルの方程式に基づく電磁気学の確立、ローレンツ因子の由来とは？①

前回記事：特殊相対性理論における相対性原理の数学的な記述と球面の方程式との関係

関連記事：ローレンツ因子とは何か？ローレンツ因子γのピタゴラスの定理を用いた導出と宇宙船内で生じる時間の遅れの実際の計算

「物理学」のカテゴリーへ

「数学」のカテゴリーへ