存在の多数性論駁④存在が無限大へと至る議論の問題点
前回は、
存在の無限小と無限大をテーマとした
ゼノンの多数性論駁の後半の議論である
存在が無限大へと至る議論において、
ゼノンの論法にそのまま従うと、
存在の中には、一定の大きさを持った無限に多くの部分があるので、
その存在の全体は無限大に大きいことになる
という議論を紹介しました。
しかし、
この論法には、その論理展開の中に
少しおかしなところがあるようにも思えます。
つまり、
たとえ、存在の中に無限に多くの部分を見つけ続けることができるとしても、
そのことによって、
その存在全体の大きさが無限大であるとは言えないのではないか?
ということです。
そこで、今回は、
この問題、すなわち、
ゼノンの多数性論駁の議論における、
存在が無限大へと至る議論の問題点について考えてみたいと思います。
存在が無限大へと至る議論の問題点
前回の議論で考えた通り、
存在が無限大へと至る議論におけるゼノンの論法では、
すべての存在は、それが一定の大きさを持つものである限り、
無限の部分を持つということが説明されます。
そして、
その議論の流れの中で、確かに、
存在の各部分がそれぞれ一定の大きさを持つ
ということは説明されているのですが、
その存在の内の
それぞれの部分同士の大きさの関係については
何の説明も証明もされていません。
したがって、この場合、
存在の各部分が一定の大きさを持っているということの意味は、
すべての部分が同じ大きさを持っているということではなく、
すべての部分がそれぞれある特定の大きさを持っている
という意味になります。
すると、確かに、
その存在の内に、
無限に多くの部分を見つけ出すことができ、
すべての部分がそれぞれある特定の大きさを持つ限り、
新たな部分が見つけ出され、
その部分の大きさが新たに追加されていくことによって、
部分の総和としての
元の存在全体の大きさが無限に増えていく
と考えるとことは可能なのですが、
新たに見つけ出さる部分によって
元の存在全体の大きさが増えていく
その大きさの増え方は、
ゼノンが主張しているよりも
だいぶ小さいということが考えられるのです。
リンゴの実が持つ無限の部分の話
例えば、
リンゴの実のような目に見える大きさの物体が有する
部分についての探究を進めていくとき、
はじめのうちに発見される部分は、
リンゴの皮であったり、果実の部分であったり、
果実の中の蜜の部分であったりと、
その部分自体も目に見える大きさの
比較的大きくて見つけやすい部分ということになります。
そして、次に、
さらに、小さな部分を見つけ出そうとしていくと、
リンゴの果実の中にある維管束(水や養分の通路)や、
その維管束を形成している
木部(道管、水の通り道)、師部(師管、栄養分の通り道)、
形成層(活発に細胞分裂を行い、植物の成長を担う部分)
といった植物組織を見つけていくことができるわけですが、
それ以上に細かい小さな部分を見つけていこうとすると、
新たに見つけ出される部分の大きさは、
急速に小さくなっていくことになります。
上記のような各植物組織は、そのそれぞれが、
多くの植物細胞を部分として持っていることになりますが、
その植物細胞は、より小さな一定の化学構造をもった
有機化合物を部分として持っていることとなります。
ここら辺からは、普通の顕微鏡どころか、
電子顕微鏡まで持ち出さないと見えないほどの
ミクロの世界の話になっていきますが、
その有機化合物や無機化合物を構成している部分として、
19世紀になると、分子が発見され、
さらに、その分子は、
原子というより小さな部分によって構成されていることが
分かっていきました。
そして、
20世紀になると、その原子の中にも、
原子核と電子というより小さな部分があり、
原子核の中には、陽子と中性子が、
20世紀の半ばにさしかかると、
さらに、それらを構成している
クォークなどの素粒子が発見されることになります。
以上のように、
少なくとも、概念上においては、
存在のさらに小さい部分を見つけ出していく探究の過程を
無限に続けていくことは可能であるわけですが、
このとき、
大きな部分の方が、より早く目につき、
より簡単に発見されやすいので、
存在の部分を次々に発見していく無限の過程においては、
新しく発見されていく部分の大きさは、後になればなるほど、
どんどん小さなものになっていくということになります。
そして、このように、
次々に、見つけ出されていく部分の数が無限にあっても、
部分の大きさがどんどん小さな大きさのものになっていく場合、
新たな部分の大きさの追加によって
元の存在の全体が無限に大きくなっていくあり方は、
ゼノンが言うほどには、勢いよく大きくなってはいかず、
その大きさは、無限大へと至るどころか、
それよりもずっと小さな有限の値へしか向かっていかない
と考えられることになるです。
有限の大きさへと無限に大きくなっていく
新たな部分の大きさが次々に無限に追加されていきながら、
追加される部分の大きさがどんどん小さなものになっていく場合、
部分の総和としての
元の存在全体の大きさの増え方はどのようになっていくのか?
ということについて分かりやすく捉えるために、
例えば、
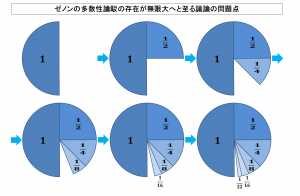
ある存在の内に見出されたはじめの部分の大きさを1として、
それ以降は、次々に、
前の大きさの半分の大きさをもった部分が無限に見つけ出されていく
というケースについて考えてみることにしましょう。
この場合、
元の存在の大きさは、新しい部分が見つけ出されていくにしたがって
無限に大きくなっていくことにはなりますが、
その無限に大きくなっていくあり方は、
という増え方となり、
以上のような、
新しい部分の大きさの無限の追加に伴う
元の存在全体の大きさの増え方を図示すると以下のようになります。
上記の図を見れは明らかな通り、
この存在全体の大きさが近づいていく値は、
無限大への拡散ではなく、
はじめの部分の大きさである1の二倍である
2という有限の値への収束に過ぎないということになります。
つまり、確かに、
その存在の内に、
新たな部分を無限に見つけ出していくことができるということは、
その部分の大きさがゼロではない以上、
部分の総和としての存在全体の大きさは、
無限に大きくなっていくと考えることはできるのですが、
それは、決して、
無限大へと無限に大きくなっていくわけではなく、
特定の有限の大きさへと向かって
無限に大きくなっていくに過ぎないということです。
以上のように、
存在の無限小と無限大をテーマとした
ゼノンの多数性論駁の後半の議論である
存在が無限大へと至る議論の方は、
存在が無限に大きくなっていくと考えることができる
ということには間違いはないのですが、
存在が無限に大きくなっていくからといって、
それが必ずしも、無限大へと大きくなっていくということは意味しない
という点において、
その論理展開に問題があると考えられるのです。
・・・
ちなみに、
存在の無限小と無限大をテーマとした
ゼノンの多数性論駁の前半の議論である
非存在が無限に多く集まっても、それはどこまで行っても
その全体が非存在であるに過ぎない
ということを示していて、
その論理展開には、明確な誤りを指摘することはできないので、
こちらの存在の多数性論駁の議論の方は、
その全体が正しい議論として保持されていると考えられます。
・・・
このシリーズの前回記事:存在の多数性論駁③無限大であると同時に無限小である
関連テーマの次回記事:素粒子の世界とゼノンの無限小の粒子、そして唯心論哲学へ
このシリーズの次回記事:
二分法のパラドックスとゴールに永久にたどり着けないランナーの話
「エレアのゼノン」のカテゴリーへ