アキレスと亀のパラドックス①無限数の点と無限回の試行回数
今回の「アキレスと亀のパラドックス」の議論は、
前回の「二分法のパラドックス」の議論の
進化版ということになるので、
議論の内容も、その問題点も二分法の議論と
本質的には同じところに帰着することになるのですが、
まずは、
今回取り上げるアキレスと亀の話の
具体的な内容について見てみることにしましょう。
『イリアス』の俊足の英雄と、『イソップ物語』の亀
アキレス(Achilles、ギリシア語ではAchilleus(アキレウス))は、
ギリシア神話に登場する
無双の力と俊足の脚を誇った英雄で、
ホメロスの叙事詩『イリアス』(Ilias、英語ではIliad(イリアッド)、トロイア軍とギリシア軍との10年にわたる戦争のうちの最後の50日間を描く、ギリシア最古の長編叙事詩)
の主人公でもありますが、
その俊足の英雄アキレスと、鈍足の亀が、
イソップ物語の「ウサギと亀」の話のように、
かけっこ勝負をしようという話になるのです。
ちなみに、
「アキレスと亀のパラドックス」の作者である
エレアのゼノンは、紀元前5世紀中頃のギリシアの哲学者であるのに対して、
『イリアス』の作者とされるホメロスは、
紀元前8世紀末に活躍した吟遊詩人、
『イソップ物語』の作者とされるイソップ(ギリシア語ではアイソーポス)は、
紀元前6世紀前半に活躍した寓話作家とされているので、
一応、ゼノンは、両者の作品を見聞きしていて、
それらの話を念頭に置いたうえで、
このパラドックスの議論を考えたと推測されます。
アキレスが直前の亀の位置に来た時、現在の亀は常にその先にいる
それでは、いよいよ本題に入りまして、
「アキレスと亀のパラドックス」の議論が
具体的にどのようなものなのかイメージしてみると、
それは、以下のような議論となります。
アキレスと亀が、かけっこ勝負をすることになり、
俊足のアキレスと鈍足の亀とのハンデとして、
亀は、アキレスよりも少し先の地点からスタートすることにします。
かけっこをする距離や時間に特に制限はなく、
アキレスが亀に追いつき、追い越すことができれば
アキレスの勝ち、
亀がいつまでもアキレスに追いつかれずに先行し続けることができれば
亀の勝ち
というルールなので、
亀よりも足が速いアキレスは、
いずれは亀を追い越すことができるのが自明の理とばかりに、
余裕のスタートを切ることになります。
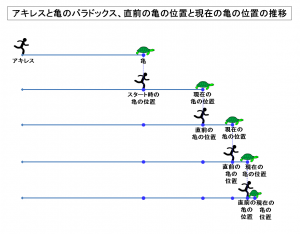
アキレスが亀に追いつき、追い越すためには、
まずは、現在の亀がいる位置まで到達しなければなりません。
そこで、アキレスは、はじめに、
スタート時に亀がいた位置を目標にして走っていくことになります。
アキレスが、スタート時に亀がいた位置に到着すると、
かけっこのスタートからアキレスが現在の地点に到達するまでの間に、
亀の方も少しだけ先へ進んでいることになるので、
今度は、アキレスは、自分より少し先にいる現在の亀がいる位置を目標にして
走っていくことになります。
そして、先ほどの亀の位置にアキレスが到達すると、
アキレスが先ほどの地点から、現在の地点に到達するまでの間に、
亀の方もわずかながら先へ進んでいることになるので、
今度も、アキレスは、自分よりわずかに先にいる現在の亀がいる位置を
新たな目標として走っていくことになります。
こうして、
アキレスが、現在の亀がいる位置を目標にして走っていくと、
その位置にアキレスが到達したとき、
アキレスよりも亀の方が常にほんの少しだけ先に進んでいることになるので、
直前に亀がいた位置に到達するたびに、
新たに現在の亀がいる位置を目標にして走っていく
という行為を繰り返す限り、
この行為は際限なく続いていくことになり、
いつまで経っても、アキレスは亀を追い越すどころか、
亀に追いつくことすらできない
ということになるのです。
無限数の点と無限回の試行回数
議論を整理してまとめると以下のようになります。
上図に示した通り、
アキレスが亀に追いつくためには、それ以前に、
現在の亀の位置まで到達しなければなりませんが、
アキレスが直前の亀の位置まで到達したとき、
常に現在の亀はアキレスより先にいることになるので、
アキレスが直前の亀の位置に到達するたびに、
次に到達すべき現在の亀の位置という新たな目標が
無限に生じ続けることになり、
アキレスは、現在の亀の位置に到達するという行為を
無限の回数成し遂げなければ、
亀に追いつくことはできないということになります。
そして、
無限の回数の行為を成し遂げるには
無限の時間が必要になるので、
アキレスは亀に永遠に追いつくことができない
という結論が帰着することになるのです。
さらに言えば、
亀に追いつくのに
無限の試行回数がかかるのに対して、
アキレスを人間と考えると※、
その寿命は有限なので、
人間としてのアキレスは、
亀に追いつこうとする無限の試行を繰り返している途中で
寿命が尽きて力尽きてしまうので、
アキレスは亀に追いつくことができないまま非業の死を遂げ、
アキレスと亀のかけっこ勝負は、
亀の勝ちと決定することにもなります。
※神話の中のアキレスは、アキレス腱の語源ともなっているように、誕生後に、母テティスによって、冥府を流れる川の神水に浸されたことで、そのときにつかまれていた足首の部分以外は不死身になっていたので、亀との永遠に終わらないかけっこの途中で、神話の結末通りに、誰かがアキレスの踵を矢で射ぬいてくれない限り、本当にアキレスが死んでくれるのかは、厳密には不明確ということになるかもしれませんが、結局、この論法に従う限り、アキレスが亀に永遠に追いつけないということは確かなので、こうしたアキレスの不死性が、「アキレスと亀のパラドックス」の議論の本筋に影響を与えることはないと考えられます。
・・・
以上のように、
前回の「二分法のパラドックス」では、
無限の数の目標地点を目指すという
無限数の点の通過問題として捉えられていた運動のパラドックスが、
今回の「アキレスと亀のパラドックス」では、
亀に追いつく行為という
無限回の試行回数の議論へと置き換えられる形で
捉え直されているということになります。
そして、
無限数の点の通過も、無限回の行為の試行も、そのどちらについても、
有限の時間のなかでは、そのすべてを完遂することは不可能なので、
走者は永久にゴール地点にたどりつけず、
アキレスは亀に永遠に追いつけない
という
ゼノンの運動のパラドックスの議論が
完成することになるのです。
・・・
このシリーズの前回記事:
二分法のパラドックスとゴールに永久にたどり着けないランナーの話
このシリーズの次回記事:
アキレスと亀のパラドックス②数学的な解決法と、哲学的問題としての本質
「エレアのゼノン」のカテゴリーへ