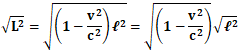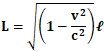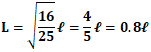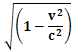ローレンツ収縮と相対性理論における物体の長さの縮み方の公式の具体的な導き方とは?相対性理論で物体の長さが縮む原理④
「相対性理論において物体の長さが縮む原理」や「ローレンツ収縮とエーテル理論」の記事で書いたように、アインシュタインの特殊相対性理論や、それに先駆けて、等速運動を行っている物体における運動方向への長さの短縮を予見したローレンツ収縮と呼ばれる理論においては、
一般的に、光速に近い速度で等速運動する物体は、静止状態にある場合よりも長さが縮んで観測されると考えられることになります。
そして、前回書いたように、そうした光速に近い速度で運動する物体において観測される長さの縮み方は、
数学や物理学において一般的な公式である「速さの公式」に対して相対性理論における時間の遅れを示す関係式を適用することによって具体的に計算することができると考えられることになるのですが、
こうして得られた物体の長さについての関係式からは、さらに、その式をより適切な形へと変形させていくことによって、
ローレンツ収縮および相対性理論における物体の縮み方の割合を示す公式を導き出すことができると考えられることになるのです。
ローレンツ収縮と相対性理論における物体の縮み方の割合の公式の導出
詳しくは前回の記事で書いたように、中学校の数学でも習う物体の移動における速さ・時間・距離の関係を示す関係式である
速さv×時間t=距離(長さ)L
という公式を地球上から観測される光速に近い等速運動の状態における物体の長さLと、同じ物体の静止状態における長さℓのそれぞれについて適用した場合、
光の速さをc、地球上の観測における時間をt、宇宙船内における時間をt’とおくと、
そして、上記の二つの関係式を相対性理論における時間の遅れを示す関係式である
(ct’)2=(vt’)2+(ct)2
という関係式に代入して式を展開していくと、
(cℓ)2=(vℓ)2+(cL)2
という相対性理論における物体の長さの縮み方を示す関係式が得られることになります。
そして、ここからさらに、上記の物体の長さについての関係式を等速運動の状態において観測される物体の長さLについてまとめていく形で変形していくと、
上記の式は以下のような形で展開していくことができると考えられることになります。
(cℓ)2=(vℓ)2+(cL)2
c2ℓ2=v2ℓ2+c2L2
c2L2=c2ℓ2‐v2ℓ2
ここで、両辺をc2で割ると、
となり、ここで、上記の式の両辺を平方根に開くと、
最終的に、等速運動の状態において観測される物体の長さLと、同じ物体の静止状態における長さℓの間には、
という関係が成り立つことになります。
そして、上記の式こそが相対性理論およびローレンツ収縮の理論において生じる物体の縮み方の割合を示す公式であると考えられることになるのです。
上記の物体の縮み方の公式を用いた宇宙船の長さの短縮の実際の計算
ここで例えば、
前回例として挙げた光速の60パーセントの速度である秒速約18万キロメートルで航行する宇宙船を相対的な静止状態にある地上から観測した場合に生じる長さの縮み方について、
今回導出した上記の相対性理論における物体の縮み方の割合を示す公式を用いることによって、改めて改めて計算し直すと、それは以下のようになると考えられることになります。
条件より、
上記の相対性理論における物体の縮み方の割合を示す公式
光の速さc=300000、宇宙船の速度v=180000を代入すると、
ここで、![]() なので、
なので、
つまり、
地球から見た場合、光速の60パーセントの速度である秒速約18万キロメートルで航行する宇宙船の長さは、静止状態における長さの0.8倍に縮んだ長さで観測されるとと計算されることになるのです。
・・・
以上のように、
ローレンツ収縮および相対性理論における物体の縮み方を示す公式は、
等速運動の状態にある物体の長さをL、静止状態における物体の長さをℓとしたうえで、物体の運動速度をv、光の速さをcとした場合、
一般的に、
という形で表記することができると考えられることになります。
つまり、
相対性理論およびローレンツ収縮の理論においては、上記の
という係数に比例する形で、光速に近い速度で等速運動する物体は、静止状態にある場合よりも長さが縮んで観測されることになると考えられることになるのです。
・・・
次回記事:ローレンツ因子の二つの表記の違いとは?時間と空間の伸縮を司る係数としてのローレンツ因子の意味
前回記事:相対性理論における物体の長さの縮み方を具体的に算出する方法とは?相対性理論において物体の長さが縮む原理③
「物理学」のカテゴリーへ
「数学」のカテゴリーへ