相対性理論における物体の長さの縮み方を具体的に計算する方法とは?相対性理論において物体の長さが縮む原理③
前回書いたように、光速に近い速度で航行する宇宙船を地球上から観測した場合、宇宙船内の中央地点の光源から発せられた光は、先に宇宙船の後方に到達してから、そののち少し遅れて宇宙船の前方へと到達することになり、
光が後方に到達してから前方に到達するまでの時間差の間に宇宙船が移動する距離の分だけ宇宙船の長さが静止状態よりも縮んで観測されるといった現象が生じることになります。
そして、こうしたことから、一般的に、相対的に静止状態にある慣性系から光速に近い速度で等速度運動を行っている物体を観測した場合、観測の対象となる物体の長さは物体の運動方向に対して縮んで観測されると考えられることになるのですが、
それでは、こうした光速に近い速度で運動する物体の長さは、物体が移動する速度の速さに対して具体的にはどれくらいの割合で縮んで観測されることになるのでしょうか?
こういった問題については数学や物理学などの分野において一般的な「速さの公式」を、このシリーズの四回前の記事で具体的な論証を行った相対性理論における「時間の遅れを示す関係式」に対して用いることによって、
そうした相対性理論における物体の長さの縮み方を示す関係式を比較的簡単に導き出すことができると考えられることになります。
相対性理論における物体の長さの縮み方を示す関係式の具体的な導出方法
物体の移動における速さ・時間・距離の関係を表す関係式である「速さの公式」は、中学の数学でも習う通り、一般的に、
速さ×時間=距離(長さ)
という形で表記することができると考えられることになります。
すると、例えば、前回取り上げた宇宙船の例のように、光速に近い速度で航行する宇宙船を地球上から観測した場合に生じる進行方向に対する宇宙船の長さの縮み方について考える場合、
まず、
地球上からの観測において長さが縮んで観測されることになる光速に近い速度で航行する宇宙船の長さをL、光の速さをcとしたうえで、その長さL分の距離を光が進むのにかかる地球上の観測における時間をtとおくと、
上記の縮んで観測される宇宙船の長さ、光の速さc、地球上の観測における光の移動時間>の三者間には、上記の速さの公式に基づいて、以下のような関係が成り立つと考えられることになります。
ct=L
そして、この式を地球上の観測における時間tについてまとめると
![]()
という関係式が得られることになります。
それに対して、
宇宙船内における観測においては、慣性の法則に基づいて、宇宙船の長さは静止状態において宇宙船の長さと同じように観測されることになるので、
静止状態における宇宙船の長さをℓ、光の速さをcとしたうえで、その長さℓ分の距離を光が進むのにかかる宇宙船内における時間をt’とおくと、この三者の間には、
![]()
という関係式が成立することになります。
そして、
以前に、「特殊相対性理論における時間の遅れのピタゴラスの定理を用いた計算方法」の記事で考察したので、ここでは詳しい説明は省きますが、
上記の宇宙船がx軸方向に秒速vキロメートルの速度で等速直線運動を行っているとしたすると、光の速さをcたうえで、地球上における時間をt、宇宙船内における時間をt’とおくと、
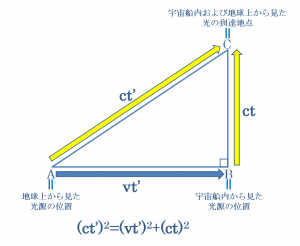
その宇宙船においては、以下の図で示したような関係式が成立すると考えられることになります。
そして、この
(ct’)2=(vt’)2+(ct)2
という関係式に、
上記の速さの公式に基づいて得られた
![]() と
と ![]() という二つの式を代入すると、
という二つの式を代入すると、
(ct’)2=(vt’)2+(ct)2
![]() となり、
となり、
ここで両辺にc2をかけると、
(cℓ)2=(vℓ)2+(cL)2
という関係式が得られることになります。
そして、この関係式こそが、相対性理論に基づいて光速に近い速度で運動する物体において観測されることになる物体の長さの縮み方の具体的な割合を示す関係式であると考えられることになるのです。
光速の60パーセントの速度で航行する宇宙船における長さの縮み方の計算
ここで、実際に、上記の関係式を用いて、相対性理論に基づいて生じることになる光速に近い速度で運動する物体において観測される物体の長さの縮み方を計算してみることにします。
すると、例えば、
光速cを秒速30万キロメートルとしたうえで、上記の例に挙げた宇宙船が光速の60パーセントの速度にあたる秒速約18万キロメートルで等速直線運動をしているとした場合、
この宇宙船において観測される地上から見た場合の長さの縮み方は、上記の関係式にc=300000と、v=180000を代入することによって具体的に計算することができると考えられることになります。
すると、
(cℓ)2=(vℓ)2+(cL)2
(300000ℓ)2=(180000ℓ)2+(300000L)2 となり、
ここで、両辺を100002で割って計算を進めていくと、
(30ℓ)2=(18ℓ)2+(30L)2
900ℓ2=324ℓ2+900L2
900L2=576ℓ2
L2=0.64ℓ2
L=0.8ℓ
となり、
以上の計算結果から、
地球上からの観測において、光速の60パーセントの速度で航行する宇宙船における長さLは、静止状態にある宇宙船の長さℓの0.8倍の長さに縮んだ状態で観測されることになると結論づけられることになるのです。
・・・
次回記事:ローレンツ収縮と相対性理論における物体の長さの縮み方の公式の具体的な導き方とは?相対性理論で物体の長さが縮む原理④
関連記事:特殊相対性理論における時間の遅れのピタゴラスの定理を用いた計算方法
前回記事:光速に近い速度で飛ぶ宇宙船の長さが静止状態よりも縮んで観測される理由とは?相対性理論において物体の長さが縮む原理②
「数学」のカテゴリーへ
「物理学」のカテゴリーへ