光速に近い速度で飛ぶ宇宙船の長さが静止状態よりも縮んで観測される理由とは?相対性理論において物体の長さが縮む原理②
前回書いたように、ガラス張りの宇宙船内のちょうど中央地点に光源を配置し、その光源から発せられた光が到達すると発光する仕組みとなった点灯ライトを宇宙船の一番前の先頭部分と一番後ろの後尾部分の合計二か所に配置したうえで、
宇宙船が静止状態にある場合と、光速に近い速度で等速度運動している場合のそれぞれのケースについて、上記の二つのライトが点灯する様子を地球上から観測した場合、
静止状態においては、ちょうど同一時刻に点灯していた前方と後方のライトが、光速に近い運動状態の場合には、後方のライトの方が先に点灯して前方のライトがそれに遅れて点灯しているように観測されることになります。
そして、前回は、こうした光速に近い速度で航行する宇宙船内における二つのライトの点灯の観測のあり方について、
前方と後方のライトが点灯する時刻の違いという時間関係における差異について考察しましたが、
それに対して、今度は、ライトが点灯するまでの間に光が進んだ距離の方に注目して考えるてみると、以下のような新たな発見が得られることになると考えられることになります。
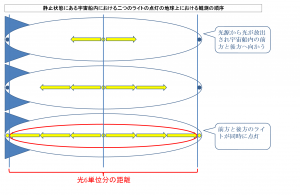
静止状態にある宇宙船の長さと光が進む距離の長さとの関係
まず、静止状態にある宇宙船における二つのライトの点灯を地球上から観測した場合、
前回考えたように、中央部の光源から発せられた光が宇宙船の前方と後方に配置されたそれぞれのライトに到達するのは同一時刻となり、ライトは二つとも同時に点灯することになりますが、
このとき、下図において示したように、
前方と後方のライトが同時に点灯するまでに光が進んだ距離の長さは、宇宙船自体の長さとぴったり一致することになります。
そして、仮に、下図において示したように、静止状態の宇宙船内において光が進んだ距離を六分割して表し、分割されたそれぞれの部分の長さを光一単位の長さとして捉えるとすると、
光速度不変の原理に基づいて、下図における光一単位の長さはどのような慣性系においても常に同一の長さとして観測されると考えられることになります。
つまり、
上記のような光が進んだ距離の長さを尺度とした物体の長さの測り方の基準に従うと、
上記の静止状態にある宇宙船は光六単位分の長さをしていると捉えられることになるのです。
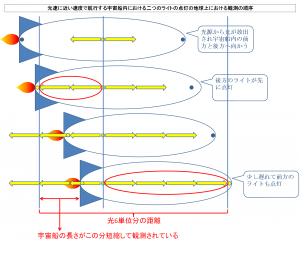
光速に近い速度で航行する宇宙船の長さが静止状態よりも縮んで観測される理由とは?
それに対して、
上記のものとまったく同じ宇宙船が、今度は光速に近い速度で航行している状態で地球上から観測されるとすると、
前回考察したように、宇宙船の移動に伴って、後方のライトは光源に近づいていくのに対して、前方のライトは光源から遠ざかってしまう分だけ、後方のライトの方が先に点灯して、そののち、前方のライトの方が遅れて点灯することになります。
すると、下図において示したように、
このとき、例えば、光源からちょうど光が二単位分進んだときに後方のライトが点灯したとすると、光速度不変の原理に基づいて二つのライトが点灯するまでに光が進む距離は宇宙船が静止状態にある場合と同じく光六単位分の距離で変わりがないので、後方のライトが点灯してからさらに光が二単位分進んで合計光が四単位分進んだときに前方のライトが点灯することになり、
光が進んだ合計六単位分の距離は、上述した静止状態にある宇宙船の長さである光六単位分の長さと一致することになります。
そして、この場合、
光六単位分の長さは、宇宙船の後方のライトが点灯した時点における後方ライトの位置と、そののち、前方のライトが点灯した時点における前方ライトの位置との距離の長さと一致するのであって、
後方ライトと前方ライトの点灯が同時に観測されない以上、それは、宇宙船自体の長さとは一致しないと考えられることになります。
つまり、
光速に近い速度で航行する宇宙船を地上から観測する場合、上記の静止状態における宇宙船の長さである光六単位分の長さは、宇宙船自体の長さではなく、後方ライトの点灯の後に前方ライトが点灯するという時間差を経て観測される光が進む距離を表すことになるのであって、
後方のライトが点灯してから前方のライトが点灯するまでの時間差が生じている間に前方へと移動してしまっている宇宙船の移動距離の分だけ、
地球上からの観測においては、光速に近い速度で航行する宇宙船の長さは短縮されて観測されることになると考えられることになるのです。
・・・
以上のように、
光速に近い速度で航行する宇宙船を地球上から観測した場合、
宇宙船の後方のライトが点灯してから前方のライトが点灯するまでの時間差の間に宇宙船自体が移動する距離の分だけ、
地球上からの観測においては、光速に近い速度で航行する宇宙船の長さが静止状態よりも縮んで観測されるという帰結が生じると考えられることになります。
そうすると、次に、こうした光速に近い速度で運動する物体の長さは、物体が移動する速度の速さに応じて、具体的にはいったいどのくらい縮んで観測されることになるのか?ということが問題となりますが、
それについては、前々回の記事でピタゴラスの定理を用いることによって導出した相対性理論において生じる時間の遅れ方の公式と、物理学における一般的な速さの定義の公式を用いることによって、
比較的簡単に導き出すことができると考えられることになるのです。
・・・
次回記事:相対性理論における物体の長さの縮み方を具体的に計算する方法とは?相対性理論において物体の長さが縮む原理③
前回記事:相対性理論ではどのような原理によって物体の長さが縮むのか?①光速に近い速度で飛ぶ宇宙船内の二つのライトの点灯の観測
関連記事:ローレンツ因子とは何か?ローレンツ因子γのピタゴラスの定理を用いた導出と宇宙船内で生じる時間の遅れの実際の計算
「物理学」のカテゴリーへ