対当関係に分類される四つの推論形式の種類のまとめ、直接推論に分類される推論の形式⑥

このシリーズの初回から前回までの五回にわたる記事で書いてきたように、

①全称肯定命題・②特称肯定命題・③全称否定命題・④特称否定命題という四つの命題形式の間には、

矛盾対当・反対対当・小反対対当・大小対当と呼ばれる四つの種類の対当関係と呼ばれる推論関係が成立すると考えられることになります。

今回は、こうした対当関係に分類される四つの推論形式の種類におけるそれぞれの概念の具体的な定義ついて、改めて図解していく形でまとめ直しておきたいと思います。

 

対当関係に分類される四つの推論形式の種類のまとめ

このシリーズの初回の記事でも書いたように、伝統的な論理学においては、全称・特称と肯定・否定という論理学的な意味における命題の量と質の違いに基づいて、

一般的に、命題の種類は、

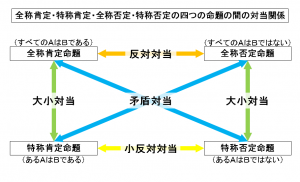
①全称肯定命題（すべてのＡはＢである）
②特称肯定命題（あるＡはＢである）
③全称否定命題（すべてのＡはＢではない）
④特称否定命題（あるＡはＢではない）

という全部で四種類の命題の区分へと分類することができると考えられることになります。

そして、上図において示したように、

こうした四種類の命題の間には、矛盾対当・反対対当・小反対対当・大小対当と呼ばれる全部で四種類の対当関係と呼ばれる推論関係が成立すると考えられることになります。

このうち、まず、上記の二番目の図の冒頭に記した矛盾対当とは、

①全称肯定命題と④特称否定命題、および、②特称肯定命題と③全称否定命題の間に成立する推論関係であり、

例えば、「すべての馬は動物である」という全称肯定命題が真であるとするならば、「ある馬は動物ではない」という特称否定命題は偽であることが必然的に帰結し、

「ある馬は魚類である」という特称肯定命題が偽であるとするならば、「すべての馬は魚類ではない」という全称否定命題は真であることが必然的に帰結するように、

矛盾対当においては、いずれか一方の命題が真ならば他方は必ず偽であり、その反対に、いずれか一方の命題が偽ならば他方は必ず真となるという命題同士の普遍的な真偽関係が成立することになります。

・・・

そして、次に記した反対対当とは、

①全称肯定命題と③全称否定命題の間に成立する推論関係であり、

例えば、「すべての馬は動物である」という全称肯定命題が真であるとするならば、「すべての馬は動物ではない」という全称否定命題は偽であることが必然的に帰結するのに対して、

「すべての馬は栗毛である」という全称肯定命題が偽であるとしても、そこから「すべての馬は栗毛ではない」という全称否定命題が真であるということは必ずしも帰結しないように、

反対対当においては、いずれか一方の命題が真ならば他方は必ず偽となるが、それとは反対に、いずれか一方の命題が偽であるとしても他方が真であるとは限らないという命題同士の普遍的な真偽関係が成立することになります。

・・・

また、その次に記した小反対対当とは、

②特称肯定命題と④特称否定命題との間に成立する推論関係であり、

例えば、「ある人間が不死である」という特称肯定命題が偽であるとするならば、「ある人間は不死ではない」という特称否定命題は真であることが必然的に帰結するのに対して、

「ある人間が男である」という特称肯定命題が真であるとしても、そこから「ある（特定の別の一人の）人間が男ではない」という全称否定命題が真であるということは必ずしも帰結しないように、

小反対対当においては、いずれか一方の命題が偽ならば他方は必ず真となるが、それとは反対に、いずれか一方の命題が真であるとしても他方が偽であるとは限らないという命題同士の普遍的な真偽関係が成立することになります。

・・・

そして、上図の最後に記した大小対当とは、

①全称肯定命題と②特称肯定命題、および、③全称否定命題と④特称否定命題との間に成立する推論関係であり、

例えば、「すべての神は不死である」という全称肯定命題が真であるとするならば、「ある神は不死である」という特称肯定命題も真であることが必然的に帰結し、

「ある人間は不死である」という特称肯定命題が偽であるとするならば、「すべての人間は不死である」という全称肯定命題も偽であることが必然的に帰結するように、

大小対当においては、全称命題が真ならば特称命題も真となり、特称命題が偽ならば全称命題も偽となるという命題同士の普遍的な真偽関係が成立することになるのです。

・・・

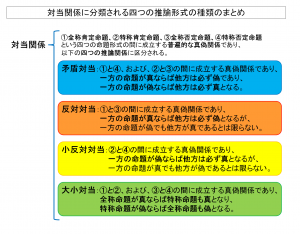
以上のことから、冒頭に挙げた図表においてまとめて示したように、

①全称肯定命題・②特称肯定命題・③全称否定命題・④特称否定命題という四つの命題形式の間に成立する

矛盾対当・反対対当・小反対対当・大小対当という四種類の対当関係は、それぞれ、

矛盾対当は、①と④、および、②と③の間に成立する、一方の命題が真ならば他方は必ず偽であり、一方の命題が偽ならば他方は必ず真となる真偽関係、

反対対当は、①と③の間に成立する、一方の命題が真ならば他方は必ず偽となるが、一方の命題が偽でも他方が真であるとは限らない真偽関係、

小反対対当は、②と④の間に成立する、一方の命題が偽ならば他方は必ず真となるが、一方の命題が真でも他方が偽であるとは限らない真偽関係、

大小対当は、①と②、および、③と④の間に成立する、全称命題が真ならば特称命題も真となり、特称命題が偽ならば全称命題も偽となる真偽関係

として定義することができると考えられることになるのです。

・・・

次回記事：

初回記事：全称・特称と肯定・否定という量と質の違いに基づく四種類の命題区分、論理学における量と質の意味とは？

前回記事：大小対当とは何か？対当関係における四つの真偽関係の違い④、直接推論に分類される推論の形式⑤

「論理学」のカテゴリーへ