直接推論（直接推理）における七つの推論の種類とは？四つの対当関係と三つの命題変換形式のまとめ、直接推論の推論の形式⑦

前回までの一連のシリーズで考察してきたように、論理学における演繹的推論には、推論の前提となる命題の数の違いに応じて、直接推論（直接推理）と間接推論（間接推理）と呼ばれる二つの推論の種類があり、

直接推論（直接推理）においては、一つの前提のみからの直接的な推論によって結論が導き出されるのに対して、間接推論（間接推理）においては、二つ以上の前提からの段階的な推論によって結論が導き出されるという点に、両者の推論のあり方の違いがあると考えられることになります。

そして、このうちの直接推論（直接推理）に含まれる具体的な推論のあり方の種類としては、

換位・換質・換質換位と呼ばれる三つの命題変換形式と、

矛盾対当・反対対当・小反対対当・大小対当と呼ばれる四つの対当関係という

合わせて七つの直接推論の種類が挙げられると考えられることになります。

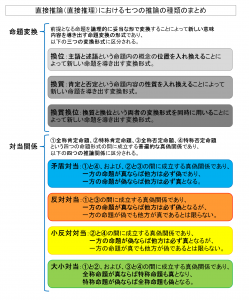
直接推論（直接推理）における七つの推論の種類のまとめ

上図において示したように、直接推論（直接推理）における具体的な推論のあり方には、

前提となる命題を論理的に妥当な形で変換することによって新しい意味内容を導き出すという直接的な命題変換に基づく推論と、

全称肯定命題（すべてのＡはＢである）、特称肯定命題（あるＡはＢである）、全称否定命題（すべてのＡはＢではない）、特称否定命題（あるＡはＢではない）という四つの命題形式の間に成立する普遍的な真偽関係のことを意味する対当関係に基づいてなされる推論という

大きく分けて二つの直接推論のパターンがあり、

このうち、

命題変換は、換位・換質・換質換位と呼ばれる三つの命題変換形式へ、

対当関係は、矛盾対当・反対対当・小反対対当・大小対当と呼ばれる四つの推論関係へとさらに細分化する形で区分することができると考えられることになります。

そして、こうした全部で七つの直接推論の種類について、それぞれの概念の定義と推論の具体例を提示していく形で改めてまとめていくと、それは以下のようになります。

換位・換質・換質換位という三つの命題変換形式の定義と具体例

まず、上図の一番上に記した命題変換の形式である換位とは、

主語と述語という命題内の概念の位置を入れ換えることによって新しい意味内容をもった命題を導き出す変換形式であり、

例えば、

「すべての天使は不死である」という前提となる命題から、「不死なるものの一部は天使である」という新しい命題を導き出すような推論が換位を用いた推論の具体例として挙げられることになります。

・・・

次に、もう一つの命題変換の形式である換質とは、

肯定と否定という命題内容の性質を入れ換えることによって新しい意味内容をもった命題を導き出す変換形式であり、

例えば、

「心は物質的存在ではない」という前提となる命題から、「心は非物質的存在である」という新しい命題を導き出すような推論が換質を用いた推論の具体例として挙げられることになります。

・・・

そして、三番目の命題変換の形式である換位換質とは、

換質と換位という両者の変換形式を同時に用いることによって新しい意味内容をもった命題を導き出す変換形式であり、

例えば、

「すべての神は非物質的存在である」という前提となる命題から、「すべての物質的存在は神ではない」という新しい命題を導き出すような推論が換質換位を用いた推論の具体例として挙げられることになります。

矛盾対当・反対対当・小反対対当・大小対当という四つの対当関係の定義と具体例

そして、上図の下部の冒頭に示した対当関係である矛盾対当とは、

全称肯定命題と特称否定命題、および、特称肯定命題と全称否定命題の間に成立する、一方の命題が真ならば他方は必ず偽であり、一方の命題が偽ならば他方は必ず真となる真偽関係であり、

例えば、

「すべての神は不死である」という全称肯定命題が真であることから、「ある神は不死ではない」という特称否定命題は偽であることを導き出し、

「ある人間は不死である」という特称肯定命題が偽であることから、「すべての人間は不死ではない」という全称否定命題は真であることを導き出すような推論が矛盾対当に基づく推論の具体例として挙げられることになります。

・・・

次に、二番目に示した対当関係である反対対当とは、

全称肯定命題と全称否定命題の間に成立する、一方の命題が真ならば他方は必ず偽となるが、一方の命題が偽でも他方が真であるとは限らない真偽関係であり、

例えば、

「すべての馬は動物である」という全称肯定命題が真であることから、「すべての馬は動物ではない」という全称否定命題は偽であることを導き出すような推論が反対対当に基づく推論の具体例として挙げられることになります。

・・・

そして、三番目に示した対当関係である小反対対当とは、

特称肯定命題と特称否定命題の間に成立する、一方の命題が偽ならば他方は必ず真となるが、一方の命題が真でも他方が偽であるとは限らない真偽関係であり、

例えば、

「ある馬は栗毛である」という特称肯定命題が偽であることから、「ある馬は栗毛ではない」という特称否定命題は真であることを導き出すような推論が小反対対当に基づく推論の具体例として挙げられることになります。

・・・

そして最後に、四番目に示した対当関係である大小対当とは、

全称肯定命題と特称肯定命題、および、全称否定命題と特称否定命題の間に成立する、全称命題が真ならば特称命題も真となり、特称命題が偽ならば全称命題も偽となる真偽関係であり、

例えば、

「すべての神は不死である」という全称肯定命題が真であることから、「ある神は不死である」という特称肯定命題が真であることを導き出し、

「ある人間は不死である」という特称肯定命題が偽であることから、「すべての人間は不死である」という全称肯定命題が偽であることを導き出すような推論が小反対対当に基づく推論の具体例として挙げられると考えられることになるのです。

・・・

次回記事：三段論法とは何か？大前提・小前提・結論という三つの命題と一つの媒概念によって構成される間接推論の形式

初回記事：直接推論と間接推論の違いとは？演繹的推論の二つの分類とそれぞれの推論のあり方の具体例

前回記事：対当関係に分類される四つの推論形式の種類のまとめ、直接推論に分類される推論の形式⑥

「論理学」のカテゴリーへ