相対性理論における時間の遅れが日常世界において観測できない具体的な理由とは？ボールと列車と光の速度の比較

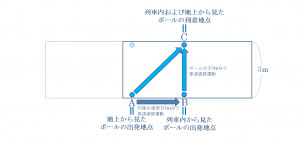
前回書いたように、ガラス張りの列車の車内で投げられたボールの運動を、地上にある展望台の上から見下ろして観測した場合、

地上から見たボールの軌道は、ボールが移動し終わるまでの間に車両が動いた距離の分だけ、列車内で見たボールの運動よりも長く斜めに進んでいるように観測され、移動距離が長くなった分だけ、ボールの速度もより速く観測されることになります。

そして、特殊相対性理論においては、それと同様に、光の進み方の場合においても、静止状態にある慣性系から等速度運動の状態にある別の慣性系における光の進み方を観測する場合、

光の軌道は等速度運動の状態にある慣性系が移動した分だけより長く斜めに進んでいるように観測されることになり、

光速度不変の原理が働く光においては、その分だけ、速度ではなく時間の方がゆっくりと進んでいるように観測されると考えられることになります。

しかし、人間の日常生活の内においては、上記の列車の例のように、走行中の乗り物などの内の人や物の動きが目の前を素早く過ぎ去っていくように観測されるといった経験は数多くあっても、

特殊相対性理論に基づく光の進み方の観測の違いによって実際に時間の進み方が遅れて観測されるといった経験をすることはまったく無いように思われるわけですが、

今回は、こうした相対性理論において生じているはずの時間の遅れが人間の日常の世界においては観測されない理由について、

前回取り上げたボールと列車と光という三つの対象の速度を比較していくことを通じて、より具体的な形で示してみたいと思います。

列車内のボールの運動においてボールが到着するまでの間に列車が動く距離の計算

まずは、前回取り上げたガラス張りの列車において行われているキャッチボールの際の野球のボールの運動の観測のされ方について、具体的な速度の数値を例に挙げてあてはめたうえで改めて考えてみることにします。

すると、例えば、

上記のガラス張りの列車の幅が3mで、列車の運行速度と、その列車内で二人の子供がキャッチボールをして投げ合っている野球のボールの速度が共に時速30～40km程度だったとした場合、

30～40km/h
=30000～40000m/3600s
=8.33～11.11m/s

となり、列車の運行速度とボールの速度は共には秒速に直すと秒速10m程度の速度ということになります。

そして、次に、

上記の走行中の列車内においてボールが列車幅分の距離である上図に示したB地点からC地点までの3mの距離を移動するのにかかる時間は、

3m÷10m/s＝0.3s　より、

0.3秒ということになり、

ボールがB地点からC地点まで移動する0.3秒間の間に、秒速10mで走っている列車自体は、

10m/s×0.3s＝3m

つまり、3m前に進んでいると考えられることになります。

そして、以上の計算結果に基づいて、地上から見た場合の上記のガラス張りの列車内におけるボールの運動の観測のされ方についてまとめると、

それは、ボールが列車幅分の距離を移動する間に列車が3m前に進んでいる分、

上図の斜めの矢印で示されているように、ボールの軌道は目に見えて大きく斜めに動いているように観測されることになり、

その分、ボールの速度も、列車内で見た場合よりもかなり速く観測されると考えられることになるのです。

ボールと列車と光の速度の比較と光が到達するまでの間に列車が動く距離の計算

それに対して、これが野球のボールではなく、光の進み方の場合には、具体的にどのようなことになるのか？ということですが、

例えば、

上記の例で挙げたガラス張りの列車の列車内において、野球のボールの代わりに光が同じような形で進んで行くと考える場合、

上記のガラス張りの列車の運行速度とボールの速度である秒速10mと光の速さである秒速30万kmを比べると、

300000km/s÷10m/s
＝300000000m/s÷10m/s
＝30000000（3000万）

となり、

つまり、列車が走る速度も、キャッチボールで投げる野球のボールの速度も光の速さと比べるとおよそ3000万分の一に過ぎない速度ということになります。

そしてさらに、より具体的な形で比較を進めていくと、

光が上記のガラス張りの列車の幅である3メートルの距離を移動するのにかかる時間は、

3m÷300000000m/s=0.00000001s

となり、それは1億分の1秒に過ぎないということになります。

そして、

その1億分の1秒の間に、上記の時速30～40km＝秒速10mの列車が移動する距離は、

10m/s×0.00000001s
＝0.0000001m（メートル）
=0.0001mm（ミリメートル）
=0.1µm（マイクロメートル）
=100nm（ナノメートル）

となるので、

つまり、光が上記の列車幅分の距離を移動する1億分の1秒の間に、列車自体が移動する距離はわずか1万分の1mm＝0.1マイクロメートル＝100ナノメートルに過ぎないということになります。

ちなみに、100ナノメートルというと、ちょうど冬にはやる流行性感冒の原因となるインフルエンザウイルスの大きさが80～120ナノメートルくらいということになるので、

光が上記の列車幅の距離を移動する間に、列車はウイルス1個分の長さも進んでいない、つまり、ほとんどまったく前に進んでいないと考えられることになるのです。

・・・

以上のように、

列車の中で投げられたボールの運動といった人間が日常生活の内で経験する一般的な物体の運動においては、

列車内でボールが投げられてからもう一方の側にボールが到着するまでの間に、ボールが位置している慣性系である列車が目に見えるだけの十分に長い距離を移動することができるために、

地上から見た場合、ボールが到着するまでの間に列車が移動した距離の分だけボールの速度が速くなっているように観測されることになるのに対して、

光の進み方の場合には、上記の場合と同じ速度で走っている列車内であっても、列車内のもう一方の側に光が到着するまでの間に列車が動く距離はほとんどゼロに近い距離となってしまい、

光が到達するまでの間に、光がその内に位置している慣性系である列車はほぼ止まったままであると結論づけられることになります。

つまり、

相対性理論において生じているはずの時間の遅れが人間の日常の世界においては観測されない理由としては、

正確に言うと、日常の世界においても相対性理論に基づいて生じる時間の遅れは理論上は生じていると考えられることになるのですが、

光の速さに対して、地球上で人間が生活を営んでいる日常の世界における物体の移動の速さがあまりに遅すぎるので、そうした地球上における物体の移動が光の進み方の観測のされ方に与える影響は事実上皆無となってしまい、

そうした相対性理論の原理に従って生じている時間の遅れを実際に体感することは事実上不可能となってしまっているということが理由として挙げられると考えられることになるのです。

・・・

次回記事：相対性理論において光の到達の遅れが時間の遅れに直結する理由とは？

前回記事：相対性理論において時間の遅れが生じる具体的な仕組みとは？野球のボールと光の進み方の違い

「物理学」のカテゴリーへ