二つの円と一つ直線に接する円は全部で何個描けるのか？①具体的なルール説明とアポロニウスの問題との関係

幾何学の分野において、ある特定の位置関係にある図形に接する円の数を求めていく問題としては、古代ギリシアの数学者にして天文学者あったアポロニウスによって提起された3つの円に接する円の数を求めていくアポロニウスの問題が有名ですが、

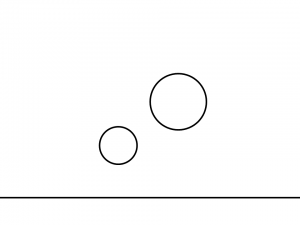
そうした古代ギリシアのアポロニウスの問題によく似た数学的な問題としては、以下の図において示したような問題についての言及がしばしばなされることがあります。

その問題というのは、

互いに少しずつ段差がつけられた形で配置された大きさの異なる二つの円とその下に位置する一つの直線に接する円は全部でいくつ描けるのか？

という問題です。

ちなみに、数学において、

円が接するというのは、二つの円または一つの円と直線が互いに交わらずに一点だけで接することを意味することになるので、

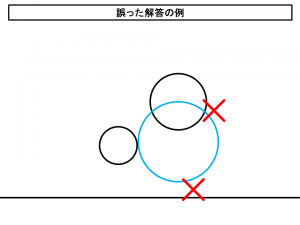
例えば、下記の図において示したような円の場合、

この解答の円は左の円とは接しているものの、右の円とは二点で交わっているので接しておらず、下の直線とも離れているため接していないので、これは誤った解答の例ということになります。

また、数学において直線とは端点を持たずにずっとまっすぐに無限に伸びていく線のことを意味していて、数学における直線や円は太さを持たないことになっているため、

鉛筆で描く円の太さをどんどん太くしていって無理やり円の厚みで両方の円に接するように描くというのもルール違反ということになります。

それでは、これで問題の基本的なルール説明は終わりとして、あとは、この問題をまだ自分で解いたことがない人は、気分転換や頭の体操を兼ねて一人でじっくりと考えていくか、

あるいは、友達や親子で競争するようにして、どのような円のパターンを描いていくことができるのか？と考えていくと楽しいと思うのですが、

次回の記事では、こうした二つの円と一つの直線に接する円について考える問題において見いだされていくことになる八つの円のパターンの具体的な解答例について順番に詳しく考察していってみたいと思います。

・・・

また、この問題を解くときのヒントというほどのことではないのですが、

この問題についてじっくりと考えていくと、きっと幾何学的なセンスや論理的な思考に長けた人ならば、四つから五つくらいまでの円のパターンを発見していくことができると考えられることになります。

まずは、そのくらいの数がこの問題における数学的な思考あるいは幾何学的な考え方の一つの合格ラインとして、

そこからさらに、

六つ目と七つ目、そして、八つ目の円を見つけ出していくためには、

この問題の原型にあるアポロニウスの問題の作者であるアポロニウスが数学者であると同時に天文学者でもあったように、

ある意味では、

宇宙的な規模にまで思考を広げていくことによって、今までには見えていなかった新たな円を見いだしていくことができると考えられることになるのです。

・・・

「数学」のカテゴリーへ

│HOME│

サブコンテンツ