二つの円と一つ直線に接する円は全部で何個描けるのか？②八つの円の具体的な解答例と宇宙的な規模で描かれる図形

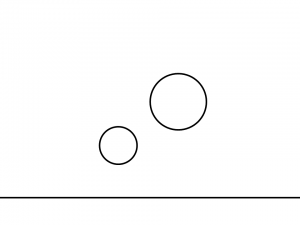
前回の記事で書いたように、幾何学の分野においては、しばしば、下記の図において示したような図形同士の関係において、

二つの円と一つ直線に接する円は全部で何個描けるのか？という問題についての言及がなされることがあります。

この問題を解く際の具体的なルール説明と、若干の問題のヒントとなるような考え方については、すでに前回の記事で書いたので、

この問題をまだ自分で解いたとがない人は、そちらの記事も参考にしてもらいつつ、どのようなパターンの円を見つけ出していくことができるのか、まずは自分の頭でじっくりと考えていくと楽しいと思いますが、

今回の記事では、さっそく、

こうした二つの円と一つの直線に接する円について考える問題において見いだされていくことになる八つの円のパターンの具体的な解答例について実際に円を描いていく形で詳しく考えていきたいと思います。

解答例1：左の円の左下と右の円の右上に内接する円

そうすると、まず、

この問題について考えていった時に、一般的に見つけていくことができると考えられる四つから五つくらいまでの円のパターンのなかでも、

比較的見つけやすいものとしては、

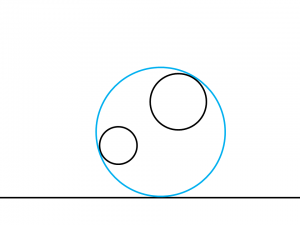
上記の図において示したような形で二つの円を自らの内に含む円、

すなわち、

左の円の左下と右の円の右上に内接する円を描いていくことができると考えられることになります。

解答例2：左の円の右下と右の円の左下に外接する円

また、その反対に、

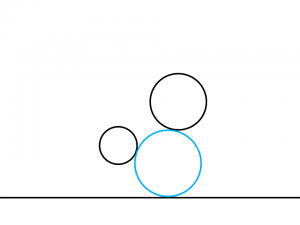
上記の図において示したような形で二つの円と自分の外側で接する円、

すなわち、左の円の右下と右の円の左下で外接する円も描いていくことができると考えられることになります。

解答例3：左の円の左上に内接して右の円の左下に外接する円

そして、そのほかにも、比較的見つけやすい円のパターンとしては、

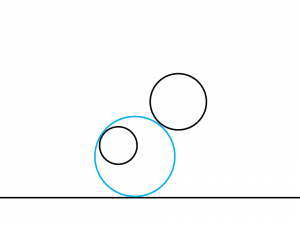
上記の図において示したように、

左の円の左上に内接して右の円の左下に外接する円も描いていくことができます。

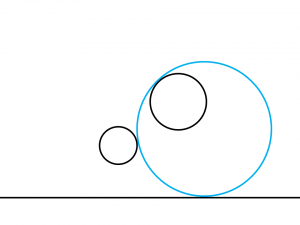
解答例4：左の円の右側に外接して右の円の左上に内接する円

そして、それとは対称的に、

上記の図において示したように、

左の円の右側に外接して右の円の左上に内接する円も描いていくことができると考えられることになります。

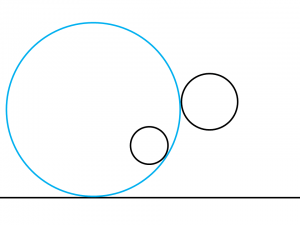
解答例5：左の円の右下に内接して右の円の左側に外接する円

また、その他にも、

上記の図において示したように、

左の円の右下に内接して右の円の左側に外接する円といった円のパターンも見いだしていくことができると考えられることになるのです。

・・・

そして、

ここからは、かなり難易度が高くなっていくことになるのですが、視界をぐっと広げて、さらにずっと巨大な円のパターンについて考えていくと、

例えば、以下のような円のパターンも描いていくことができると考えられることになります。

解答例6：左の円と右の円の左上に外接する円

視点をずっと後ろへと引いていって、

直線がどこまでも伸びていく先を考えていくと、

上記の図において示したような左の円と右の円の左上に外接する巨大な円を描いていくことができると考えられることになります。

解答例7：左の円と右の円の右下に内接する円

また、それと同じような考え方に基づいて、

上記の図において示したような左の円と右の円の右下に内接する巨大な円を描いていくこともできると考えられることになります。

・・・

そして、最後に、視界をさらに広げていって、

宇宙的な規模にまで思考を広げていくと、この問題の最後の答えとなる第八の円の姿が目の前に現れていくことになります。

解答例8：左の円の上側に外接して右の円の下側に内接する円

そうすると、まず、

こうした左の円の上側に外接して右の円の下側に内接する円というのは、一見すると、どんなに円を大きく描いてもすぐに上へと離れて行ってしまって直線には接することがないようにも思えてしまうことになるのですが、

上記の図において示したように、

二つの円のうちの大きい方の円よりも直径にしてさらに100倍ほど大きい巨大な円を考えていくことによって、

そうした二つの円と一つの直線に接する第八の円を見いだしていくことができると考えられることになるのです。

太陽と月と地球といった天体同士の関係を連想させる宇宙的な規模において描かれていくことになる八つの円の姿

ちなみに、天文学との関係で言えば、

こうしたおよそ100倍という壮大な規模にある大きさの関係としては、

月と地球との大きさの関係は、直径にして約4倍、体積にして約50倍の差があるのに対して、

地球と太陽との大きさの関係は、直径にして約100倍、体積にして約130万倍の差があるといった宇宙における天体同士の関係のあり方が連想されることになると考えられることになります。

つまり、そういった意味では、

こうした二つの円と一つ直線に接する円を求めていくというシンプルな幾何学の問題のうちには、太陽と月と地球といった天体同士の関係を連想させるような一つの宇宙を見いだしていくことができるとも考えられ、

この問題において、ある意味では宇宙的なスケールにおいて描かれていくことになる八つの円たちの姿は、数学的な意味だけではなく、芸術的な意味においても興味深い図形となっていると考えられることになるのです。

・・・

次回記事：英雄テーセウスの誕生と海の神ポセイドンとアテナイの王という二人の父親の存在、ギリシア神話の英雄テーセウスの物語①

前回記事：二つの円と一つ直線に接する円は全部で何個描けるのか？①具体的なルールの説明とアポロニウスの問題との関係

「数学」のカテゴリーへ