特殊相対性理論における相対性原理の数学的な記述と球面の方程式との関係
前回書いたように、1905年にアインシュタインが発表した特殊相対性理論においては、
光速度不変の原理と、すべての慣性系における物理法則の相対性原理という二つの原理を基盤として現代物理学の新たな基礎となる物理学理論が組み立てられていくことになります。
そして、こうした二つの原理に基づいて、相対性理論の中で最も有名な数式であるE=mc2といった質量とエネルギーの等価性を示す式も導出されることになるのですが、
それでは、こうした特殊相対性理論における光速度不変の原理と相対性原理は、数学的な記述としては、具体的にはどのような形で記述することができ、
そうした相対性原理の数学的記述から、どのような形で時間や空間や質量の伸び縮み、そして、E=mc2といった特殊相対性理論における重要な物理学的帰結が導き出されていくことになると考えられることになるのでしょうか?
光速度不変の原理の数学的な記述と球面の方程式
はじめに、特殊相対性理論において最も基盤となる原理である光速度不変の原理がどのような形で数学的に記述することができるのか?ということについてですが、
まず、光速度不変の原理とは、より正確に言えば、光の速度がすべての慣性系(静止状態か等速運動状態にある座標系)におけるあらゆる観察者にとって光源の動きと関係なく不変であることを示す原理ということになります。
そして、それは、より具体的な状況に即して考えると、例えば、以下のような物理的状況を示す原理であると考えられることになります。
例えば、
tを時間、cを光の速度としたうえで、
t=0の時点では原点が一致する慣性系Sと慣性系S’があり、
慣性系S’は、慣性系Sに対してx軸方向に速度vで等速運動をしていると考えることにします。
すると、このとき、
t=0の瞬間に慣性系Sの原点から光が等方向的に放たれたとすると、
その光は光速度不変の原理に基づいて、慣性系Sにおいても慣性系S’においても同等に等方的に速度cで伝達されていくことになるので、
光は、慣性系Sにおける時刻tの時点においては距離r=ctの球面上の地点に到達していて、それに対応する慣性系S’における時刻t’の時点においては距離r=ct’の球面上の地点に到達していると考えられることになります。
ところで、ここで、
こうした空間および時間の座標系における球面上の任意の点の座標の数学的記述のあり方について考えると、それは高校数学で出てくる球面の方程式によって記述することができると考えられることになります。
高校数学の数学Bの分野における「空間の方程式」と題される項目では、三次元空間における直線や平面の方程式と並んで、球面の方程式の記述方法が説明されていて、そこでは、
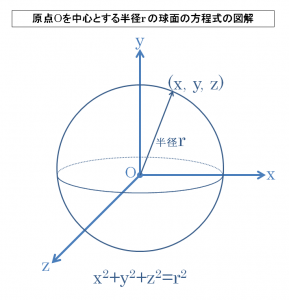
原点を中心とする半径r の球面の方程式は
x2+y2+z2=r2
という式で表現されることになります。
相対性原理の数学的な記述とローレンツ変換
それに対して、
三次元空間を示す座標である(x, y, z)に、時間座標であるtを加えた相対性理論が扱う四次元の時空座標においては、
慣性系Sにおける時刻tの時点における光の到達地点を示す時空座標を(x, y, z, t)として記述すると、そこには上記の球面の方程式に基づいて、
x2+y2+z2=(ct)2
という関係が成り立ち、
それと同様に、
慣性系S’における時刻t’の時点における光の到達地点を示す時空座標を(x’, y’, z’, t’)として記述すると、そこには、
x’2+y’2+z’2=(ct’)2
という関係が成り立つことになります。
そして、上記の式を右辺が0になるようにして各項を並べ替えると、
慣性系Sについては、
x2+y2+z2=(ct)2
(ct)2-x2-y2-z2=0
慣性系S’については、
x’2+y’2+z’2=(ct’)2
(ct’)2-x’2-y’2-z’2=0
となり、両者の式を一つにまとめると、
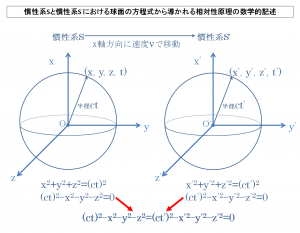
(ct)2-x2-y2-z2=(ct’)2-x’2-y’2-z’2=0
という式が得られることになり、
これが光速度不変の原理に基づいてすべての慣性系において光の運動を含むあらゆる物理法則が同じ構造の数学的形式によって記述することができるとする
特殊相対性理論における相対性原理の数学的な記述であると考えられることになるのです。
・・・
以上のように、
特殊相対性理論における相対性原理の数学的な記述は、上記の
(ct)2-x2-y2-z2=(ct’)2-x’2-y’2-z’2=0
という式によって記述することができると考えられることになりますが、
上記の相対性原理を示す式においては、光の速さが不変である代わりに、今度は、光の速度の方を基準として、それに基づいて、空間や時間の方が伸び縮みしていくことが必要になると考えられることになります。
そして、詳しくは次回述べるように、
慣性系S における時空座標(x, y, z, t)と慣性系S’における時空座標(x’, y’, z’, t’)における両者の座標を同じ構造の数学的形式によって対応づけ、
上記の相対性原理を示す式において示されている空間や時間の伸び縮みの構造をより具体的な形で記述していくためには、
慣性系S と 慣性系S’におけるxとx’、yとy’、zとz’、tとt’というそれぞれの座標同士を関連づける普遍的な座標の変換の形式として、
ローレンツ変換と呼ばれる二つの慣性系間の座標の変換形式が求められることになりことになるのです。
・・・
次回記事:ローレンツ変換とは何か?特殊相対性理論の相対性原理の方程式に基づくローレンツ変換の導出とローレンツ因子の意味
前回記事:特殊相対性理論と一般相対性理論の違いとは?相対性理論における「特殊」と「一般」の意味
「物理学」のカテゴリーへ
「数学」のカテゴリーへ