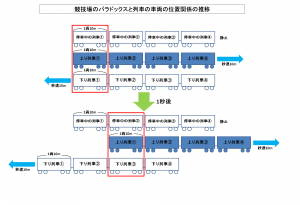
競技場のパラドックス①列車の右側では、左側よりも時間が速く進む

前回までの３回にわたる
「アキレスと亀のパラドックス」についての考察を終え、

今回からは、

ゼノンの運動のパラドックスにおける
新しいパラドックスの議論である

「競技場のパラドックス」（または、動いている列のパラドックス）
の議論へと入っていくわけですが、

ここら辺の議論から、

ゼノンがパラドックスの議論によって
論駁する対象が広がっていき、

その批判と吟味の矛先が、運動の概念だけでなく、

運動を成り立たせている前提にある
時間概念の方へと、

向け変えられていくことになります。

列車の右側では、左側よりも時間が2倍速く進む

今回紹介するゼノンの議論は、
競技場のパラドックス、または、より抽象的な形で、
動いている列のパラドックスとも呼ばれている議論で、

正確に言うと、

馬車の車列や、より一般的な意味での物量体の列が
互いにすれ違っていく状況で生じる
運動のパラドックスを示す議論なのですが、

基本的には、現代で言うならば、

複数の列車の車両のようなものが動いていくことにより、
互いの車両の位置関係が順次変わっていく状態をイメージすればいいと思います。

そして、

「競技場のパラドックス」の議論について、
実際に自分が列車の車両に乗っているつもりで、具体的にイメージしてみると、
それは、以下のような議論になります。

上り列車の両隣にはそれぞれ
停車中の列車と下り列車が位置していて、はじめの状態では、
すべての列車の１号車が左端でピッタリ揃った状態にあり、

その状態から、
上り列車は左から右へ移動し、
下り列車は反対に、右から左へと移動していきます。

そして、

すべての車両の一両の幅は10mで、
上り列車と下り列車は、共に秒速10mの速度で動き続けているとしましょう。

このような状況のもと、

あなたは、上り列車の最後尾にあたる１号車に乗っていて、
列車の進行方向を向いて座りながら、
両側の車窓に映る景色を交互に眺めています。

このとき、

電車が等速で動き続けるのに従って、
車窓に映る景色も等速で流れ続けることになり、

それは、
規則正しい時間経過を示していることになります。

例えば、

腕時計において、

数字と印が等間隔に並んだ文字盤の上を
秒針が等速で規則正しく進んで行くことによって、
1秒ずつ、1単位ずつの時間が刻まれていくように、

列車が等速で規則正しく進んで行くことによって、
車窓を等速で流れていく等間隔に並んだ車両の姿も、
1単位ずつ刻まれる時間の流れそのものを表しているということです。

はじめの状態では、
上り列車の１号車の車窓から外を見ると、
左手の車窓には、停車中の列車の１号車が、
右手の車窓には、下り列車の１号車がそれぞれ見えることになります。

そして、

今度はその1秒後に、
同じように上り列車の１号車の車窓から外を見ると、

上図を見ればわかる通り、

今度は、
左手の車窓には、停車中の列車の２号車が見えているのに対して、
右手の車窓には、下り列車の３号車が見えることになります。

つまり、

左手の車窓では、景色が１号車から２号車へと
1車両分進んでいる間に、

右手の車窓では、１号車から３号車へと
2車両分進んでしまった

ということです。

そして、

先ほどの議論の前提では、

腕時計の針の等速で規則正しい運動によって
時間が刻まれていくのと同様に、

等速で移動する列車から見える
等間隔に並んだ車両が移動していく姿は、

1単位ずつ刻まれる時間の流れそのものを表すとされていたので、

車窓から見える車両の移動のあり方は、
時間の進み方そのものでもあるということになります。

すると、

左側の車窓では、1両分の移動に対応する
1単位分の時間が進む間に、

右側の車窓では、2両分の移動に対応する
2単位分の時間が進んでいたということになり、

あなたが乗っている
列車の右側では、
列車の左側よりも2倍時間が速く進む

と考えられることになるのです。

言わば、

右側の窓際に置いてあった時計だけが
故障でもないのに急に早く進むようになり、

左側の時計の針が1単位分進む間に、
右側の時計の針はその2倍の2単位分進むようになってしまった

というように、

列車の左側と右側では、ある意味で、
時間の進み方が異なるようになってしまった
と捉えることもできるということです。

・・・

以上のように、

ゼノンの「競技場のパラドックス」（または動いている列のパラドックス）
の議論においては、

同じ列車の運動において、
左側で1単位分進む時間が右側では2単位分の時間に等しい

ということが帰結することになるのですが、

この結論は、

時間を伸び縮みせずに、どこでも同じように流れる
絶対的な客観的時間として捉える場合、

矛盾した結論ということになります。

つまり、

時間をニュートンの絶対時間のような、
絶対不変の何物にも依存しない客観的な存在として捉えると、
運動という概念自体が成立不可能となるということであり、

逆に言えば、

運動という概念が成立するためには、

時間概念自体が、

見る人の視点や、その人が置かれている状況などによって変化し、
自在に伸び縮みする相対的な概念であることを認めなければならない

という結論が帰結することになるのです。

・・・

このシリーズの前回記事：
アキレスと亀のパラドックス③無限に細かくちぎれるパンの話

このシリーズの次回記事：
競技場のパラドックス②古代ギリシア版の相対性理論

「エレアのゼノン」のカテゴリーへ