特殊相対性理論における時間の遅れのピタゴラスの定理を用いた計算方法
前回の記事で書いたように、アインシュタインの特殊相対性理論においては、
ある慣性系から、光速に近い等速運動の状態にある別の慣性系の内における光の進み方を見た場合、光が進む距離がより長くなっているように観測されるにもかかわらず、光速度不変の原理に基づいて光の速度自体は変化しないことから、
光速に近い等速運動の状態にある慣性系の内においては、光の速度ではなく時間の進み方が遅れて観測されると考えられることになります。
そこで今回は、そうした相対性理論において生じることになる時間の遅れは、具体的にどのような数式によって計算することができるのか?ということについて、
光速に近い速度で航行する宇宙船内における光の進み方を宇宙船内と地球上の双方から見た場合の観測のされ方の違いを図示することによって得られる直角三角形に対して、ピタゴラスの定理を用いて関係式をつくるという方向から考えてみたいと思います。
相対性理論における宇宙船内と地球上から見た光の進み方の違いと特殊相対性理論における時間の遅れのピタゴラスの定理を用いた計算式
例えば、
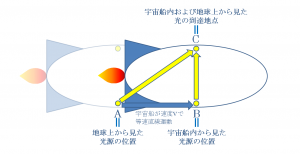
地球のすぐそばを光の速さ=cに近い速度vで等速運動している宇宙船が存在するとして、
そうした光速に近い等速運動状態にある宇宙船の慣性系に対して、地球上の観測地点における慣性系は相対的に静止した状態にあると捉えられるとします。
そして、
そうした光速に近い速度で航行する宇宙船内の一方の壁に位置する光源からもう一方の壁に位置する到達地点へと光が進んで行く進み方を、宇宙船内と地上からの双方において観測するとした場合、
まず、
宇宙船内の一方の壁からもう一方の壁へと光が到達するまでの間に、地球上からは宇宙船の移動に合わせて光源および光の到達予定地点の位置が移動して観測されることになるので、
地上から見た光放出時の光源の位置をA、宇宙船内から見た光源の位置をBとしたうえで、両者から見た光の到達地点をCとおくと、上記のA, B, Cという三つの地点の間には、上図において示した位置関係が存在すると考えられることになります。
すると、
慣性の法則に基づいて、等速運動の状態にある宇宙船内で観測される光の進み方は、静止状態にある地球上において観測される光の進み方とまったく同じように観測されることになるので、
宇宙船内において観測される上図の光源の位置Bから光の到達地点Cまでの光の進み方は、静止状態にある地球上において観測される光の進み方と同じであり、
宇宙船内においては、光が地点Bから地点Cまで進むのにかかる時間は、地球上で静止した宇宙船の船内において観測されるのとまったく同じ時間の進み方として観測されると考えられることになります。
したがって、
地球上の時間の進み方において、光が地点Bから地点Cまで進むのにかかる時間の長さをtとおくと、それと同様に、
宇宙船内の観測においては、光が光源の位置Bから光の到達地点Cまで進むのにかかる時間の長さは地球上の場合と同じtとなり、
下図において示した通り、地点Bから地点Cまでの距離は、光速c×地球上における時間t、すなわち、ctという積の形で表すことができると考えられることになるのです。
それに対して、
静止状態にある地球上から上記の光速に近い速度で航行する宇宙船の内部における光の進み方を観測した場合、
冒頭で述べたように、光の速度は一定のcのままで光の進む距離は斜めに伸びる形で観測されることになることから、時間の進み方が遅れて観測されると考えられることになります。
具体的には、地球上から観測した場合の光の進む距離は地球から見た光源の位置Aから光の到達地点Cへと斜めに伸びる形で観測されることになるので、
地球から見た宇宙船内の時間の進み方において、光が地点Aから地点Cまで進むのにかかる時間の長さをt’とおくと、
下図において示した通り、地点Aから地点Cまでの距離は、光速c×地球から見た宇宙船内の時間t’、すなわち、ct’という積の形で表すことができると考えられることになるのです。
そして、最後に、
地球から見た宇宙船内の光源の位置の移動距離である地点Aから地点Bまで距離は、宇宙船の速度v×地球から見た宇宙船内における時間t’、すなわち、vt’という積の形で表すことができると考えられることになるので、
以上のことから、
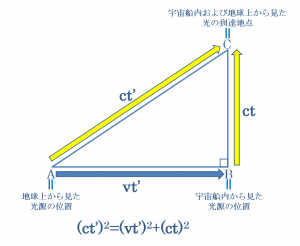
A, B, Cという三つの地点の間の距離である、線分BC、線分AC、線分ABにおいては、それぞれ、BC=ct、AC=ct’、AB=vt’という関係が成り立っていると考えられることになります。
そして、下図において示したように、
ここでさらに、上記の点A, B, Cからなる直角三角形ABCを考えると、ピタゴラスの定理を用いることによって、
AC2 =AB2+BC2
(ct’)2=(vt’)2+(ct)2
という関係式が成り立つことになり、
上記の数式が相対性理論において生じる時間の遅れの具体的な計算方法を示す数式であると考えられることになるのです。
光速の60パーセントの速度で航行する宇宙船内の時間の遅れの計算
ここで、せっかくなので、実際に、
上記のピタゴラスの定理を用いた数式を使って、実際に特殊相対性理論において生じる時間の遅れを計算してみることにします。
すると、例えば、
光速cを秒速30万キロメートルとしたうえで、上記の例で挙げた宇宙船が光速の60パーセントの速度すなわち秒速約18万キロメートルで航行しているとした場合、
上記の(ct’)2=(vt’)2+(ct)2という関係式に、光の速度c=300000と、宇宙船の速度v=180000を代入して計算すれば、
地球上における時間tに対する地球から見た宇宙船内における時間t’の時間の伸び方の割合を算出することによって、
地球上から観測されることになる宇宙船内の時間の遅れを具体的に計算することが可能であると考えられることになります。
すると、上記の条件より、
(ct’)2=(vt’)2+(ct)2
(300000t’)2=(180000t’)2+(300000t)2 となるので、
ここで、両辺を100002で割ると、
(30t’)2=(18t’)2+(30t)2 となり、この数式の計算をさらに進めていくと、
900t’2=324t’2+900t2
576t’2=900t2
t’2=1.5625t2 となります。
そしてここで、時間を表すt’は正の数なので、両辺を平方根に開くと
![]() となり、最終的に、
となり、最終的に、
![]() と算定されることになります。
と算定されることになります。
つまり、以上の計算結果に基づくと、
地球上から見た宇宙船内における時間t’は、地球上における時間tよりも1.25倍伸びた状態で観測されることになり、
地球から見た場合、光速の60パーセントの速度である秒速18万キロメートルで航行する宇宙船内においては地球上よりも1.25倍時間が遅く進むと考えられることになるのです。
・・・
以上のように、
特殊相対性理論において光速に近い等速運動の状態にある宇宙船内において生じることになる時間の遅れは、
光速をc、宇宙船の速度をv、地球上における時間をt、地球から見た宇宙船内における時間をt’、としたうえで、
宇宙船内と地球上から見た光の進み方の違いを図示した直角三角形に対してピタゴラスの定理を用いることによって得られる関係式である
(ct’)2=(vt’)2+(ct)2
という数式を用いることによって具体的に計算することが可能であると考えられることになります。
そして、前々回の記事で書いたように、より専門的には、アインシュタインの特殊相対性理論において生じる時間の遅れや空間の収縮といった現象は、
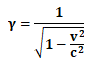
という形で表されるローレンツ因子γに比例する形で生じていると考えられることになるのですが、
こうしたアインシュタインの特殊相対性理論において必須の概念となるローレンツ因子と呼ばれる係数の値も、今回と同様のピタゴラスの定理を用いた計算式を利用することによって導出することができると考えられることになるのです。
・・・
次回記事:ローレンツ因子とは何か?ローレンツ因子γのピタゴラスの定理を用いた導出と宇宙船内で生じる時間の遅れの実際の計算
前回記事:相対性理論において時間の遅れが生じる具体的な仕組みとは?野球のボールと光の進み方の違い
「物理学」のカテゴリーへ
「数学」のカテゴリーへ