太陽視差を利用した地球と太陽の距離の計算方法とは？三角関数と直角三角形の関係を利用した地球と太陽の距離の概算

前回の記事で書いたように、観測対象となる天体を地球の中心にあたる地心から見た場合と、地球上の実際の観測地点から見た場合とでは、

地球の自転運動の影響を受けることによって、日周視差あるいは地心視差と呼ばれる観測方向の角度のずれが生じていくことになると考えられることになります。

そして、こうした日周視差や地心視差と呼ばれる視差のあり方は、地球の中心である地心と、地球上の観測地点と、観測対象となる天体という三点を結ぶ三角形が観測地点の角において90度となる直角三角形によって結ばれる地点、

すなわち、地球から見て観測対象となる天体が地平線上に沈んでいく地点に到達したときに視差が最大化することになり、その地点における視差のあり方は地平視差とも呼ばれることになるのですが、

こうした地平視差と呼ばれる視差の角度のあり方からは、太陽や月などといった地球と比較的近い距離に位置する天体との間の距離を計算していくこともできると考えられることになります。

太陽視差を利用した地球と太陽の距離の計算方法

例えば、

太陽視差と呼ばれる地球から見た太陽の地平視差のあり方は、角度の度分秒表記のあり方において、およそ8.794秒、すなわち、通常の度数表記のあり方においては0.002443度ほどの角度として観測されることになるのですが、

こうした太陽視差と呼ばれる視差の角度の値からは、具体的には以下のような形で、地球と太陽との間の距離を計算していくことができると考えられることになります。

・・・

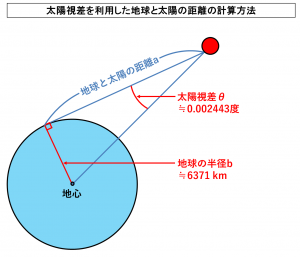
上記の図において示したように、

太陽視差と呼ばれる地球から見た太陽の地平視差のあり方が観測される地点においては、

地球の中心である地心と、地球上の観測地点と、観測対象となる天体という三点は、上記の図のような直角三角形によって結ばれることになると考えられることになります。

そして、この直角三角形においては、

直角となっている一つの角と共に、地球から見た太陽の地平視差、すなわち、太陽視差にあたるもう一つの角の角度も天体観測によって明らかとなっていって、

さらに、地球の中心にあたる地心と地球上の観測地点との間の距離は、地球の半径にあたる6371 kmと一致することになることから、そうした直角三角形の一辺の長さについても明らかとなっていると考えられることになります。

したがって、

こうした地球の中心である地心と、地球上の観測地点と、観測対象となる天体という三点を結ぶ上記の直角三角形においては、

三角形の一辺と二つの角の長さと大きさが明らかとなっていることから、三角形の定義のあり方に基づいて残りの二つの辺の長さについても計算によって導き出していくことができると考えられることになるのです。

三角関数と直角三角形の関係を利用した地球と太陽の距離の概算

具体的な計算過程を概算値を用いて示していくとすると、

地球の半径にあたる辺の部分を直角三角形の高さb＝6371 km、

太陽視差にあたる角の部分を直角三角形の底辺の角度θ＝0.002443度

としたうえで、

上記の直角三角形の底辺にあたる地球上の観測点からの地球と太陽の距離をaとした場合、

三角関数におけるtan（タンジェント）の定義から、上記の直角三角形においては、

tanθ＝b/a

という関係が成立することになると考えられることになります。

そして、任意の角度θに対するtanθの値は、上記のtanθ＝b/aという三角比の関係から逆算していくことによって、三角関数表やエクセルのTAN関数のような形で予めすべて計算によって導き出しておくことができ、

角度θ＝0.002443度のときのtanθの値は約0.00004263839になることが分かっているので、

したがって、

上記のtanθ＝b/aという基本式にこうした地球の半径bと太陽視差θのタンジェントの値をそれぞれ代入していくことによって、

tanθ＝b/a
0.00004263839＝6371/a
a＝6371÷0.00004263839
a≒149419337km

すなわち、

地球と太陽の距離a≒1億4941万9337km

という値を得ることができると考えられることになります。

そして、現代の天文学においては、

実際の地球と太陽の距離は約1億4960万kmであることが分かっているので、

上述した太陽視差と三角関数を利用した概算において求めた1億4941万9337kmという値は、こうした地球と太陽の距離をある程度正確に指し示しているということが確認できることになると考えられることになるのです。

・・・

次回記事：月の地平視差を利用した地球と月の距離の計算方法とは？太陽系内の天体の距離を概算する実用的な観測データとしての日周視差

前回記事：日周視差とは何か？地球の自転運動との関係と太陽や月における具体的な地平視差の角度

「天文学」のカテゴリーへ

「その他の雑学」のカテゴリーへ