大小対当とは何か?対当関係における四つの真偽関係の違い④、直接推論に分類される推論の形式⑤
前回までの三回の記事で書いてきたように、
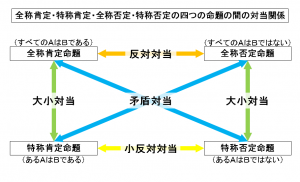
①全称肯定命題・②特称肯定命題・③全称否定命題・④特称否定命題という四つの命題形式の間には、
矛盾対当・反対対当・小反対対当・大小対当と呼ばれる四つの種類の対当関係と呼ばれる推論関係が成立すると考えられることになります。
そして、このうちの三つの対当関係である矛盾対当と、反対対当そして、小反対対当と呼ばれる推論のあり方については、それぞれ推論のあり方に関する個々の記事で詳しく考察してきましたが、
今回は、そうした前回までの考察を踏まえたうえで、上記の四つの対当関係のうちの最後の対当関係にあたる大小対当と呼ばれる推論関係の定義について、具体的な命題の例を挙げることによって詳しく考察していきたいと思います。
大小対当とは何か?真の場合は大から小へと偽の場合は小から大へと進む推論関係
まず、上図の左右において示した大小対当と呼ばれる対当関係が具体的にどのような概念として定義されることになるのか?ということについてですが、
大小対当とは、①全称肯定命題と②特称肯定命題、および、③全称否定命題と④特称否定命題との間に成立する命題同士の普遍的な真偽関係のことを意味する概念であり、
この対当関係は、「すべての~」を意味する全称命題と「ある(一部の)~」を意味する特称命題の間で成立する推論関係であることから、
それが、全称命題というより大規模な意味内容を示す命題と、特称命題というより小規模な意味内容を示す命題の間で成立する推論関係という意味で、
「大小」対当と呼ばれていると考えられることになります。
そして、
こうした大小対当の関係にある命題同士においては、全称命題が真ならば特称命題も真となり、特称命題が偽ならば全称命題も偽となるという真偽関係が成立することになります。
例えば、
「すべての人間は死すべきものである」(ずべての人間の命には限りがある)という全称肯定命題が真であるとするならば、それは、この世界の内に存在するどの一人の人間を連れて来てもその命には限りがある、つまり、この世に不死の人間などいないということを意味することになるので、
この命題と大小対当の関係にある「ある人間は死すべきものである」という特称肯定命題も真であるということが必然的に結論づけられることになります。
そして、
これが偽の命題についての推論の場合は、上記の真の命題についての推論の場合とは逆に、特称命題の方から全称命題の方へと推論が進んでいくことになるのですが、
例えば、
「ある馬が栗毛である」という特称肯定命題が偽の場合、それは、この世界には栗毛ではない馬も少なくとも一頭は存在するということを意味することになるので、
この命題と大小対当の関係にある「すべての馬が栗毛である」という全称肯定命題も当然ながら偽であると必然的に結論づけられることになります。
ちなみに、
こうした大小対当と呼ばれる推論関係における偽の命題についての推論が、真の命題についての推論の場合とは異なり、全称命題の方から特称命題の方へと推論を進めることができないことについても一応確認しておくと、
例えば、
「ずべて馬が栗毛である」という全称肯定命題が偽であるとしても、それは、この世界に存在するあらゆる馬が栗毛一色というわけではないということを意味するだけであって、
ある一頭の馬は栗毛ではなく白毛や青毛であるかもしれないが、別の一頭の馬は栗毛であるかもしれないという事態を排除するものではないので、
上記のような全称肯定命題が偽であるということだけでは、上記の命題と大小対当の関係にある「ある(特定の一頭の)馬が栗毛である」という特称肯定命題は真であるとも偽であるとも結論づけることができないと考えられることになります。
このように、大小対当においては、
真の命題についての推論の場合は、全称命題の方から特称命題の方へと推論が進んでいくのに対して、
偽の命題についての推論の場合は、その反対に、特称命題の方から全称命題の方へと推論が進んでいくことになると考えられることになるのです。
・・・
以上のように、
大小対当とは、一言でいうと、
全称命題が真ならば特称命題も真となり、特称命題が偽ならば全称命題も偽となるという全称命題と特称命題の間で成立する普遍的な真偽関係のことを意味する概念であり、
こうした大小対当と呼ばれる対当関係は、全称肯定命題(すべてのAはBである)と特称肯定命題(あるAはBである)、および、全称否定命題(すべてのAはBではない)と特称否定命題(あるAはBではない)の間で成立する推論関係として位置づけられることになります。
そして、
こうした大小対当と呼ばれる推論のあり方においては、
真の命題についての推論は、より大きな命題である全称命題から特称命題へと一方向的に進み、偽の命題についての推論は、より小さな命題である特称命題から全称命題へと一方向的に進むという意味において、
それは、真の場合は大から小へと、偽の場合は小から大へと進む推論関係のことを意味する概念として捉えることができると考えられることになるのです。
・・・
次回記事:対当関係に分類される四つの推論形式の種類のまとめ、直接推論に分類される推論の形式⑥
前回記事:小反対対当とは何か?対当関係における四つの真偽関係の違い③、直接推論に分類される推論の形式④
「論理学」のカテゴリーへ
「語源・言葉の意味」のカテゴリーへ