ローレンツ因子の二つの表記の違いとは?時間と空間の伸縮を司る係数としてのローレンツ因子の意味
以前に書いた「ローレンツ変換とは何か?」および「ローレンツ因子とは何か?」の記事において考察したように、
ローレンツ変換とは、異なる等速運動の状態にある慣性系である慣性系Sと慣性系S’の時空座標の間に成立する不変的な座標の変換関係のことを意味する変換形式であり、
相対性理論においては、光速に近い速度で等速運動する慣性系と、その慣性系に対して相対的な静止状態にある慣性系との間では、
こうしたローレンツ変換と呼ばれる座標の変換形式の内に現れるローレンツ因子の値に比例する形で、空間や時間の伸び縮みといった現象が生じると考えられることになるります。
そして、こうした相対性理論における物体の空間的および時間的な観測のされ方と深い関わりのあるローレンツ因子と呼ばれる係数の定義のあり方には、一般的に、以下で述べるような二つの表記法があると考えられることになります。
時間の伸び方を司る因子としてのローレンツ因子γ
詳しくは、「特殊相対性理論における時間の遅れ」の記事で書いたように、
慣性系Sにおける時間をt、そして、慣性系S’における時間をt’とした場合、
慣性系Sに対してx軸方向に速度vで移動している慣性系S’においては、それぞれの慣性系において観測される慣性系S’内の光の進み方の違いから、
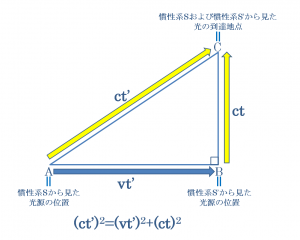
tとt’という二つの時間の間には、下図のような直角三角形として示すことができる関係が成り立つと考えられることになります。
そして、上記の直角三角形に対してピタゴラスの定理を用いることによって得られる(ct’)2=(vt’)2+(ct)2という時間についての関係式をt’について展開していくことによって、
最終的に、慣性系Sにおける時間tと慣性系S’における時間t’の間には、
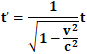
という関係式が成り立つことになり、
この関係式が相対性理論において、光速に近い速度で等速運動する物体において生じることになる時間の伸び方を表す公式ということになります。
そして、
通常のローレンツ因子の定義においては、こうした相対性理論における時間の伸び方を示す係数がローレンツ因子γ
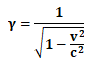
として定義されることになるのですが、
つまり、そういう意味においては、
ローレンツ因子γとは、相対性理論において、光速に近い速度で等速運動する物体において生じることになる時間の伸び方を司る因子であると考えられることになるのです。
空間の縮み方を司る因子としてのローレンツ因子α=1/γ
それに対して、
詳しくは、「相対性理論における物体の長さの縮み方」の記事で書いたように、
等速運動の状態にある物体の長さをL、静止状態における物体の長さをℓとした場合、
上記の時間の伸び方を表す公式に対して、速さv×時間t=長さ(距離)Lという一般的な速さの公式を代入することによって(cℓ)2=(vℓ)2+(cL)2という関係式が得られることになります。
そして、上記の物体の長さについての関係式をLについて展開していくことによって、
最終的に、等速運動の状態にある物体の長さをLと静止状態における物体の長さをℓの間には、
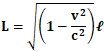
という関係式が成り立つことになり、
この関係式が相対性理論において、光速に近い速度で等速運動する物体において生じることになる物体の長さの縮み方を表す公式ということになります。
そして、
前述したローレンツ因子γに対して、こうした相対性理論における物体の長さの縮み方を示す係数がローレンツ因子α、あるいは、そのままローレンツ因子1/γ
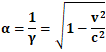
として定義されることになるのですが、
つまり、そういう意味においては、
ローレンツ因子αまたはローレンツ因子1/γとは、相対性理論において、光速に近い速度で等速運動する物体において生じることになる物体の長さの縮み方、すなわち、空間の縮み方を司る因子であると考えられることになるのです。
・・・
以上のように、
ローレンツ因子の表記法には、ローレンツ因子の一般的な定義であるローレンツ因子γのほかに、ローレンツ因子α(=1/γ)いう表記もあり、
両者の表記の違いは、時間座標あるいは空間座標といった、それぞれの因子が用いられている座標変換の局面の差異によって使い分けられることになると考えられることになります。
つまり、一言でいうと、
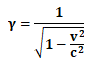
という逆数の形で示されている通常の表記におけるローレンツ因子γが、相対性理論において生じる時間の伸び方を表す因子であるのに対して、
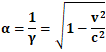
という形で表記されるローレンツ因子αあるいはローレンツ因子1/γの方は、言わば、相対性理論における空間の縮み方を表すバージョンのローレンツ因子として捉えることができると考えられることになるのです。
・・・
次回記事:なぜ相対性理論において光の速さは不変でなければならないのか?①実証的な事実としての光速度不変性
前回記事:ローレンツ収縮と相対性理論における物体の長さの縮み方の公式の具体的な導き方とは?相対性理論で物体の長さが縮む原理④
「物理学」のカテゴリーへ
「語源・言葉の意味 」のカテゴリーへ